Question

16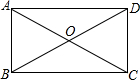．如图，矩形ABCD中，对角线AC、BD交于点O，若∠BOC=120°，AC=8，AB的长度是（　　）

• A． 4
• B． 4$\sqrt{2}$
• C． 4$\sqrt{3}$
• D． 8

Answer 1

分析 由矩形的性质得出OA=OB=4，再证明△AOB是等边三角形，得出AB=OA即可．

解答 解：∵四边形ABCD是矩形，
∴OA=$\frac{1}{2}$AC=4，OB=$\frac{1}{2}$BD，AC=BD，
∴OA=OB=4，
∵∠BOC=120°，
∴∠AOB=60°，
∴△AOB是等边三角形，
∴AB=OA=4；
故选：A．

点评 本题考查了矩形的性质、等边三角形的判定与性质；熟练掌握矩形的性质，并能进行推理计算是解决问题的关键．