题目内容
6.任意画一个四边形,以四边的中点为顶点组成一个新四边形,这个新四边形的形状是平行四边形.分析 根据三角形的中位线平行于第三边,且等于第三边的一半可得EH∥BD,EH=$\frac{1}{2}$BD.GF∥BD,GF=$\frac{1}{2}$BD,进而可得EH=GF,EH∥GF,从而可得四边形EFGH为平行四边形.
解答  解:连接BD,
解:连接BD,
∵在△ABD中,E、H是AB、AD中点,
∴EH∥BD,EH=$\frac{1}{2}$BD.
∵在△BCD中,G、F是DC、BC中点,
∴GF∥BD,GF=$\frac{1}{2}$BD,
∴EH=GF,EH∥GF,
∴四边形EFGH为平行四边形.
故答案为:平行四边形.
点评 本题主要考查了三角形的中位线的性质和平行四边形的判定,关键是掌握三角形的中位线平行于第三边,且等于第三边的一半.

练习册系列答案
相关题目
17.在数-$\sqrt{2}$,0,1,$\sqrt{2}$中,最大的数是( )
| A. | $\sqrt{2}$ | B. | 1 | C. | 0 | D. | $-\sqrt{2}$ |
18.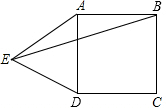 如图,在正方形ABCD的外侧,作等边三角形ADE,则∠AEB=( )
如图,在正方形ABCD的外侧,作等边三角形ADE,则∠AEB=( )
 如图,在正方形ABCD的外侧,作等边三角形ADE,则∠AEB=( )
如图,在正方形ABCD的外侧,作等边三角形ADE,则∠AEB=( )| A. | 10° | B. | 15° | C. | 30° | D. | 150° |
 如图,在?ABCD中,AC、BD相交于O,E是CD的中点,连接OE,△BCD的周长为10,则△ODE的周长为5.
如图,在?ABCD中,AC、BD相交于O,E是CD的中点,连接OE,△BCD的周长为10,则△ODE的周长为5. 如图,在△ABC中,AD是中线,△ABC面积为16,则△ADC的面积为8.
如图,在△ABC中,AD是中线,△ABC面积为16,则△ADC的面积为8.