题目内容
已知⊙O是正△ABC的内切圆,且⊙O的内接正六边形的周长为24,则△ABC的周长为( )
| A、24 | ||
| B、36 | ||
C、12
| ||
D、24
|
考点:正多边形和圆
专题:
分析:根据题意画出图形,连接OD,OE,OB,OF,根据正六边形的性质得出其边长,再根据等边三角形的性质即可得出结论.
解答: 解:如图所示,连接OD,OE,OB,OF,
解:如图所示,连接OD,OE,OB,OF,
∵⊙O的内接正六边形的周长为24,
∴DE=
=4.
∵△ODE是等边三角形,
∴OD=OE=4,⊙O的半径等于4.
∵△ABC是等边三角形,
∴∠OBF=30°,
∴BF=
=
=4
,
∴BC=2BF=8
,
∴△ABC的周长=3BC=24
.
故选D.
 解:如图所示,连接OD,OE,OB,OF,
解:如图所示,连接OD,OE,OB,OF,∵⊙O的内接正六边形的周长为24,
∴DE=
| 24 |
| 6 |
∵△ODE是等边三角形,
∴OD=OE=4,⊙O的半径等于4.
∵△ABC是等边三角形,
∴∠OBF=30°,
∴BF=
| OF |
| tan30° |
| 4 | ||||
|
| 3 |
∴BC=2BF=8
| 3 |
∴△ABC的周长=3BC=24
| 3 |
故选D.
点评:本题考查的是正多边形和圆,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
 如图,小明将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端5米处,发现绳子底端距打结处约为1米.请你设法计算出旗杆的高度.
如图,小明将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端5米处,发现绳子底端距打结处约为1米.请你设法计算出旗杆的高度.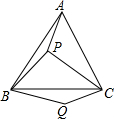 如图,P是等边△ABC内的一点,连接PA、PB、PC,以BP为一边作∠PBQ=60°且使BQ=BP,连接CQ
如图,P是等边△ABC内的一点,连接PA、PB、PC,以BP为一边作∠PBQ=60°且使BQ=BP,连接CQ 如图,在平面直角坐标系中,直线l是第二、四象限的角平分线.
如图,在平面直角坐标系中,直线l是第二、四象限的角平分线. 已知AB=AC,AD=AE,∠1=∠2,问CE=BD吗?
已知AB=AC,AD=AE,∠1=∠2,问CE=BD吗? 如图,在四边形ABED中,∠E=∠D=90°,在△ABC中,∠ACB=90°,AC=BC,其顶点C在ED上,求证:BE+AD=DE.
如图,在四边形ABED中,∠E=∠D=90°,在△ABC中,∠ACB=90°,AC=BC,其顶点C在ED上,求证:BE+AD=DE.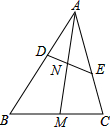 如图,在△ABC中,点D、E分别在边AB、AC上,且
如图,在△ABC中,点D、E分别在边AB、AC上,且