题目内容
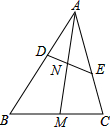如图，在△ABC中，点D、E分别在边AB、AC上，且| AD |
| AC |
| AE |
| AB |
| 1 |
| 2 |
| EN |
| BM |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：相似三角形的判定与性质
专题：
分析：首先证明△ADE∽△ACB，即可证得∠AED=∠B，然后证明△ANE∽△ABM即可根据相似三角形的性质求解．
解答：解：∵
=
=
，∠BAC=∠BAC，
∴△ADE∽△ACB，
∴∠AED=∠B，
又∵∠BAM=∠CAM，
∴△ANE∽△ABM，
∴
=
=
．
故选A．
| AD |
| AC |
| AE |
| AB |
| 1 |
| 2 |
∴△ADE∽△ACB，
∴∠AED=∠B，
又∵∠BAM=∠CAM，
∴△ANE∽△ABM，
∴
| EN |
| BM |
| AE |
| AB |
| 1 |
| 2 |
故选A．
点评：本题考查了相似三角形的判定与性质，正确理解相似三角形的判定定理是关键．
练习册系列答案
计算高手系列答案
相关题目
由于受雾霾天气影响，某药店将防雾霾口罩的价格进行两次上调．由原来的每只25元，连续两次提价a%后售价提高到每只36元，下列所列方程正确的是（ ）
| A、25（1-a%）2=36 |
| B、25（1+a%）2=36 |
| C、25（1+2a）=36 |
| D、25（1+a2%）=36 |
已知⊙O是正△ABC的内切圆，且⊙O的内接正六边形的周长为24，则△ABC的周长为（ ）
| A、24 | ||
| B、36 | ||
C、12
| ||
D、24
|
在正△ABC中，D为△ABC所在的平面内一点，当D点在平面内转动时，