题目内容
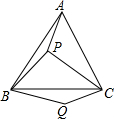 如图,P是等边△ABC内的一点,连接PA、PB、PC,以BP为一边作∠PBQ=60°且使BQ=BP,连接CQ
如图,P是等边△ABC内的一点,连接PA、PB、PC,以BP为一边作∠PBQ=60°且使BQ=BP,连接CQ(1)观察并猜想AP与CQ之间的大小关系,并证明你的结论;
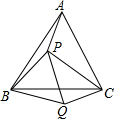
(2)若PA:PB:PC=3:4:5,连接PQ,求∠APB的度数.
考点:全等三角形的判定与性质,等边三角形的性质,勾股定理的逆定理
专题:
分析:(1)首先根据等式的性质证明∠ABP=∠CBQ,即可证明△ABP≌△CBQ,根据全等三角形的对应边相等证明;
(2)首先证明△PBQ是等边三角形,然后利用勾股定理的逆定理证明△PCQ是直角三角形,据此即可求得∠BQC,则∠APB即可求解.
(2)首先证明△PBQ是等边三角形,然后利用勾股定理的逆定理证明△PCQ是直角三角形,据此即可求得∠BQC,则∠APB即可求解.
解答:解:(1)AP=CQ.
理由是:∵△ABC是等边三角形,
∴∠ABC=60°,
又∵∠PBQ=60°,
∴∠ABP=∠CBQ,
在△ABP和△CBQ中,
,
∴△ABP≌△CBQ,
∴AP=CQ;
(2)∵PA:PB:PC=3:4:5,
∴设PA=3x,则PB=4x,PC=5x,
∵BP=BQ,∠PBQ=60°,
∴△BOQ是等边三角形.
∴∠BQP=60°,PQ=BP=4x,
所以在△PQC中,PC2=PQ2+CQ2,
∴△PCQ是直角三角形,∠PQC=90°.
∴∠BQC=60°+90°=150°,
∴∠APB=∠BQC=150°.
理由是:∵△ABC是等边三角形,
∴∠ABC=60°,
又∵∠PBQ=60°,
∴∠ABP=∠CBQ,
在△ABP和△CBQ中,
|

∴△ABP≌△CBQ,
∴AP=CQ;
(2)∵PA:PB:PC=3:4:5,
∴设PA=3x,则PB=4x,PC=5x,
∵BP=BQ,∠PBQ=60°,
∴△BOQ是等边三角形.
∴∠BQP=60°,PQ=BP=4x,
所以在△PQC中,PC2=PQ2+CQ2,
∴△PCQ是直角三角形,∠PQC=90°.
∴∠BQC=60°+90°=150°,
∴∠APB=∠BQC=150°.
点评:本题考查了全等三角形的判定与性质,根据勾股定理的逆定理证明△PCQ是直角三角形是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 由图可知,不等式组
由图可知,不等式组
|
| A、x>1 | B、-2<x<3 |
| C、x<-2 | D、1<x<3 |
由于受雾霾天气影响,某药店将防雾霾口罩的价格进行两次上调.由原来的每只25元,连续两次提价a%后售价提高到每只36元,下列所列方程正确的是( )
| A、25(1-a%)2=36 |
| B、25(1+a%)2=36 |
| C、25(1+2a)=36 |
| D、25(1+a2%)=36 |
据省统计局公布信息:今年“十一”黄金周游客,西安再创游客人数和旅游收入新高.7天我市共接待游客630.01万人次,同比增长33.3%;游客总收入29.12亿元人民币.同比增长29.47%,其中数据29.12亿元用科学记数法表示是( )
| A、2.92×10元 |
| B、2.912×109元 |
| C、2.912×108元 |
| D、2.912×107元 |
已知⊙O是正△ABC的内切圆,且⊙O的内接正六边形的周长为24,则△ABC的周长为( )
| A、24 | ||
| B、36 | ||
C、12
| ||
D、24
|
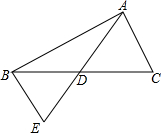 如图,△ABC中,点D是BC中点,连接AD并延长到点E,连接BE.
如图,△ABC中,点D是BC中点,连接AD并延长到点E,连接BE.