题目内容
2.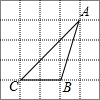 △ABC在网络中的位置如图所示,则cos∠ACB的值为( )
△ABC在网络中的位置如图所示,则cos∠ACB的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 cos∠ACB的值可以转化为直角三角形的边的比的问题,因而过点A作AD垂直于CB的延长线于点D.利用勾股定理计算出AB,在Rt△ADC中根据三角函数的定义求解.
解答 解:作AD⊥BC的延长线于点D.
在Rt△ADC中,BD=AD,则AB=$\sqrt{2}$BD.
cos∠ACB=$\frac{AD}{AB}$=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
故选B.
点评 本题考查了锐角三角函数的概念:在直角三角形中,正弦等于对边比斜边;余弦等于邻边比斜边;正切等于对边比邻边.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
13.在数轴上与-3的距离等于4的点表示的数是( )
| A. | 1 | B. | -7 | C. | -1或7 | D. | 1或-7 |
17. 与抛物线y=-2x2+12x+16关于y轴对称的抛物线的解析式为( )
与抛物线y=-2x2+12x+16关于y轴对称的抛物线的解析式为( )
 与抛物线y=-2x2+12x+16关于y轴对称的抛物线的解析式为( )
与抛物线y=-2x2+12x+16关于y轴对称的抛物线的解析式为( )| A. | y=-2x2+12x-16 | B. | y=-2x2-12x-16 | C. | y=-2x2-12x+16 | D. | y=2x2+12x+16 |
11.菱形的周长为8.4cm,相邻两角之比为5:1,那么菱形一组对边之间的距离为( )
| A. | 1.05cm | B. | 0.525cm | C. | 4.2cm | D. | 2.1cm |
 如图,是由若干个完全相同的小正方体组成的一个几何体的主视图和左视图,则组成这个几何体的小正方体的个数是5或6或7或8或9或10.
如图,是由若干个完全相同的小正方体组成的一个几何体的主视图和左视图,则组成这个几何体的小正方体的个数是5或6或7或8或9或10.