题目内容
7.先化简,再求代数式(1-$\frac{3}{x+2}$)÷$\frac{1-{x}^{2}}{x+2}$的值,其中x=2$\sqrt{3}$-(-2)0.分析 先根据分式混合运算的法则把原式进行化简,再求出x的值代入进行计算即可.
解答 解:原式=$\frac{x-1}{x+2}$•$\frac{x+2}{-(x+1)(x-1)}$
=-$\frac{1}{x+1}$,
当x=2$\sqrt{3}$-(-2)0=2$\sqrt{3}$-1时,原式=-$\frac{1}{2\sqrt{3}-1+1}$=-$\frac{\sqrt{3}}{6}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
2.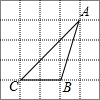 △ABC在网络中的位置如图所示,则cos∠ACB的值为( )
△ABC在网络中的位置如图所示,则cos∠ACB的值为( )
 △ABC在网络中的位置如图所示,则cos∠ACB的值为( )
△ABC在网络中的位置如图所示,则cos∠ACB的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
19.下列说法正确的是( )
| A. | 若连接四边形中点所形成的四边形是矩形,则原四边形一定是菱形 | |
| B. | 若连接四边形中点所形成的四边形是菱形,则原四边形一定是矩形 | |
| C. | 若连接四边形中点所形成的四边形是正方形,则原四边形一定是正方形 | |
| D. | 以上说法均不对 |
16.菱形的面积为36,一条对角线长为8,这里一条对角线的长为( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
 已知:如图,△ABC中,∠C=90°,∠B的平分线交AC于点D,CD=15,AD=25,求AB的长.
已知:如图,△ABC中,∠C=90°,∠B的平分线交AC于点D,CD=15,AD=25,求AB的长.