题目内容
17．
与抛物线y=-2x2+12x+16关于y轴对称的抛物线的解析式为（ ）| A． | y=-2x2+12x-16 | B． | y=-2x2-12x-16 | C． | y=-2x2-12x+16 | D． | y=2x2+12x+16 |
分析 先把抛物线配成顶点式，然后写出顶点关于y轴对称的点，把它作为所求抛物线的顶点，这样就可确定对称后抛物线的解析式．
解答 解：∵y=-2x2+12x+16=-2（x-3）2+34，顶点坐标为（3，34），
（3，34）关于y轴对称的点的坐标为（-3，34），
而两抛物线关于y轴对称时形状不变，
∴y=-2x2+12x+16关于y轴对称的抛物线的解析式为y=-2（x+3）2+34=-2x2-12x-16．
故选：B．
点评 本题考查了抛物线关于坐标轴对称的抛物线解析式求法．类似于点关于坐标轴对称的坐标求法，关于x轴对称，点横坐标不变，纵坐标变为相反数，关于y轴对称，点横坐标变为相反数，纵坐标不变．
练习册系列答案
相关题目
5．
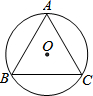如图，⊙O是等边三角形ABC的外接圆，⊙O的半径为2，则等边△ABC的边长为（ ）
如图，⊙O是等边三角形ABC的外接圆，⊙O的半径为2，则等边△ABC的边长为（ ）| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | $2\sqrt{3}$ |
12．
在直角坐标系中，我们把横、纵坐标都是整数的点叫做整点，且规定；正方形内部不包括边界上的点，如果如图所示的中心在原点，一边平行于x轴的正方形，边长为1的正方形内部有1个整点，边长为2的正方形内部有1个整数点，边长为3的正方形内部有9个整点，…，则边长为8的正方形内的整点个数为（ ）
在直角坐标系中，我们把横、纵坐标都是整数的点叫做整点，且规定；正方形内部不包括边界上的点，如果如图所示的中心在原点，一边平行于x轴的正方形，边长为1的正方形内部有1个整点，边长为2的正方形内部有1个整数点，边长为3的正方形内部有9个整点，…，则边长为8的正方形内的整点个数为（ ）| A． | 42 | B． | 40 | C． | 36 | D． | 49 |
2．
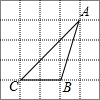△ABC在网络中的位置如图所示，则cos∠ACB的值为（ ）
△ABC在网络中的位置如图所示，则cos∠ACB的值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{3}}{3}$ |
9．计算9x3÷（-3x2）的结果为（ ）
| A． | -3x | B． | 3x | C． | -6x | D． | 3x5 |