题目内容
10.A、B、C三人参加一次游戏,A、C在同一地点,B在他们前面200米处,三人同时同向(朝前)行走,A、B的速度分别为60米/分和50米/分,当C赶上B,C马上返回迎接A;当遇到A,C再次返回追赶B,如此继续,直至A、B、C相聚在同一地点,游戏结束.若C从开始到第一次遇到A用了5分钟,求C的速度以及到游戏结束时C走了多少距离.分析 设C的速度为x米/分,C追到B的时间为y分钟,则追到B后与A相遇的时间为(5-y)分钟,根据题意列出方程组求解即可.
解答 解:设C的速度为x米/分,C追到B的时间为y分钟,则追到B后与A相遇的时间为(5-y)分钟,
根据题意得:$\left\{\begin{array}{l}{\frac{200+50y}{y}=x①}\\{\frac{200+50y-60y}{x+60}=5-y②}\end{array}\right.$
解得:$\left\{\begin{array}{l}{x=100}\\{y=4}\end{array}\right.$.
答:C的速度为100米/分钟.
点评 本题考查了应用类问题,能够找到两个等量关系是解答本题的关键,难度不大.

练习册系列答案
相关题目
20.若点C为线段Ab的黄金分割点,且AC>BC,则$\frac{BC}{AB}$的值为( )
| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{5}+1}{2}$ | C. | $\frac{3-\sqrt{5}}{2}$ | D. | $\sqrt{5}$-2 |
5.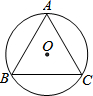 如图,⊙O是等边三角形ABC的外接圆,⊙O的半径为2,则等边△ABC的边长为( )
如图,⊙O是等边三角形ABC的外接圆,⊙O的半径为2,则等边△ABC的边长为( )
 如图,⊙O是等边三角形ABC的外接圆,⊙O的半径为2,则等边△ABC的边长为( )
如图,⊙O是等边三角形ABC的外接圆,⊙O的半径为2,则等边△ABC的边长为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
2.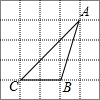 △ABC在网络中的位置如图所示,则cos∠ACB的值为( )
△ABC在网络中的位置如图所示,则cos∠ACB的值为( )
 △ABC在网络中的位置如图所示,则cos∠ACB的值为( )
△ABC在网络中的位置如图所示,则cos∠ACB的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
19.下列说法正确的是( )
| A. | 若连接四边形中点所形成的四边形是矩形,则原四边形一定是菱形 | |
| B. | 若连接四边形中点所形成的四边形是菱形,则原四边形一定是矩形 | |
| C. | 若连接四边形中点所形成的四边形是正方形,则原四边形一定是正方形 | |
| D. | 以上说法均不对 |
20.沪杭甬高速公路的主要路段是248公里长的沪杭甬高速公路和142公里长的上三高速公路,这里的248属于( )
| A. | 标号 | B. | 排序 | C. | 计数 | D. | 测量 |
 如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可供利用25m),现在已备足可以砌50m长的墙的材料.
如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可供利用25m),现在已备足可以砌50m长的墙的材料.