题目内容
20．一次函数y=（m2-4）x+（m-1）和y=（m-1）x+m-5的图象与y轴分别交于点P和点Q，若点P与点Q关于x轴对称，则m=3．分析 根据函数解析式求出P、Q的坐标，再由P点和Q点关于x轴对称可列出等式解得m的值．
解答 解：∵y=（m2-4）x+（m-1）和y=（m-1）x+m-5的图象与y轴分别交于点P和点Q，
∴P（0，m-1），Q（0，m-5）
又∵P点和Q点关于x轴对称
∴可得：m-1=-（m-5）
解得：m=3．
故答案为：3．
点评 本题考查了两条直线相交或平行问题，直线与y轴的交点坐标，以及关于x轴对称的点的坐标特征，关键在于根据函数解析式求出P、Q的坐标．
练习册系列答案
阅读快车系列答案
相关题目
11．下列各组数据中的三个数作为三角形的边长，其中能构成直角三角形的是（ ）
| A． | $\sqrt{3}$，$\sqrt{4}$，$\sqrt{5}$ | B． | 2，3，4 | C． | 6，7，8 | D． | 1，$\sqrt{2}$，$\sqrt{3}$ |
如图，四边形ABCD是矩形，将矩形折叠，使得点D落在BC边上．折痕经过点A，作出折叠后的图形（要求尺规作图，保留作图痕迹，不写作法）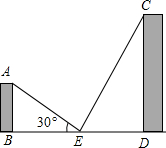
如图，两座建筑物AB与CD，其地面距离BD为60米，E为BD的中点，从E点测得A的仰角为30°，从C处测得E的俯角为60°，现准备在点A与点C之间拉一条绳子挂上小彩旗（不计绳子弯曲），求绳子AC的长度．（结果保留一位小数，$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73）
