题目内容
5.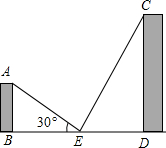 如图,两座建筑物AB与CD,其地面距离BD为60米,E为BD的中点,从E点测得A的仰角为30°,从C处测得E的俯角为60°,现准备在点A与点C之间拉一条绳子挂上小彩旗(不计绳子弯曲),求绳子AC的长度.(结果保留一位小数,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,两座建筑物AB与CD,其地面距离BD为60米,E为BD的中点,从E点测得A的仰角为30°,从C处测得E的俯角为60°,现准备在点A与点C之间拉一条绳子挂上小彩旗(不计绳子弯曲),求绳子AC的长度.(结果保留一位小数,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
分析 根据60°、30°角的余弦值可求得AE和CE,然后由勾股定理来求AC的长度即可.
解答  解:如图,连接AC.
解:如图,连接AC.
在直角△ABE中,BE=30米,∠AEB=30°,则AE=$\frac{BE}{cos30°}$=$\frac{30}{\frac{\sqrt{3}}{2}}$=20$\sqrt{3}$(米).
在直角△CDE中,EE=30米,∠CED=60°,则CE=$\frac{ED}{cos60°}$=$\frac{30}{\frac{1}{2}}$=60(米).
又∵∠AEC=180°-30°-60°=90°,
∴由勾股定理得到:AC=$\sqrt{A{E}^{2}+C{E}^{2}}$=40$\sqrt{3}$≈69.2(米).
答:AC的长度约为69.2米.
点评 本题考查了解直角三角形的应用--仰角俯角问题.要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目

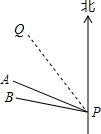 如图,台风中心位于点P处,并沿北偏西30°方向PQ移动,已知台风中心移动的速度是30km/h,受台风影响区域的半径为200km.A市位于点P的北偏西60°方向上,与点P的距离为200$\sqrt{3}$km处;B市位于点P的北偏西75°方向上,与点P的距离为210$\sqrt{2}$km处.
如图,台风中心位于点P处,并沿北偏西30°方向PQ移动,已知台风中心移动的速度是30km/h,受台风影响区域的半径为200km.A市位于点P的北偏西60°方向上,与点P的距离为200$\sqrt{3}$km处;B市位于点P的北偏西75°方向上,与点P的距离为210$\sqrt{2}$km处.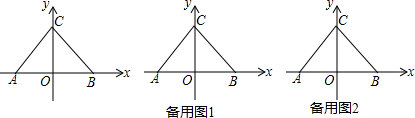
 如图,已知B、D、E、C四点在同一直线上,且AD=AE,∠1=∠2.求证:△ABC是等腰三角形.
如图,已知B、D、E、C四点在同一直线上,且AD=AE,∠1=∠2.求证:△ABC是等腰三角形. 如图,由小亮家向东走20m,再向北走10m就到了小丽家;若再向北走30m就到了小红家;再向东走40m,就到了小涛家.若用(0,0)表示小亮家的位置,用(2,1)表示小丽家的位置.
如图,由小亮家向东走20m,再向北走10m就到了小丽家;若再向北走30m就到了小红家;再向东走40m,就到了小涛家.若用(0,0)表示小亮家的位置,用(2,1)表示小丽家的位置.