题目内容
15.若m是一元二次方程方程x|a|-1-x-2=0的一个实数根.(1)求a的值;
(2)不解方程,求代数式(m2-m)•(m-$\frac{2}{m}$+1)的值.
分析 (1)根据一元二次方程的定义来求a的值;
(2)由(1)得到该方程为x2-x-2=0,把x=m代入可以求得(m2-m)、(m-$\frac{2}{m}$+1)的值;然后将其整体代入即可求得所求代数式的值.
解答 解:(1)由于x|a|-1-x-2=0是关于x的一元二次方程,所以|a|-1=2,
解得:a=±3;
(2)由(1)知,该方程为x2-x-2=0,
把x=m代入,得
m2-m=2,①
又因为m2-1-$\frac{2}{m}$=0,
所以m-$\frac{2}{m}$=1,②
把①②代入(m2-m)•(m-$\frac{2}{m}$+1),得
(m2-m)•(m-$\frac{2}{m}$+1)=2×(1+1)=4,即(m2-m)•(m-$\frac{2}{m}$+1)=4.
点评 本题考查了一元二次方程的定义和一元二次方程的解的定义.解题时,利用了整体代入是数学思想,减少了繁琐的计算过程,提高了解题的正确率.

练习册系列答案
相关题目
5.下列真命题中,它的逆命题也是真命题的是( )
| A. | 全等三角形的对应角相等 | |
| B. | 对顶角相等 | |
| C. | 等边三角形是锐角三角形 | |
| D. | 直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半 |
17.已知单项式-xm-2y3与$\frac{2}{3}$xny2m-3n是同类项,那么m,n的值分别是( )
| A. | $\left\{\begin{array}{l}{m=3}\\{n=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{m=3}\\{n=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{m=-3}\\{n=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{m=-3}\\{n=-1}\end{array}\right.$ |
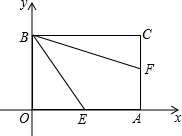 如图,四边形的顶点O在平面直角坐标系的原点,顶点A、B分别在x轴、y轴上,OB∥AC,OB=AC.
如图,四边形的顶点O在平面直角坐标系的原点,顶点A、B分别在x轴、y轴上,OB∥AC,OB=AC.
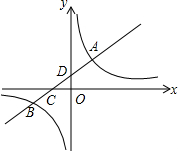 如图,一次函数y1=k1x+b(k1>0)的图象经过点C(-3,0),且与两坐标轴围成的三角形的面积为3.
如图,一次函数y1=k1x+b(k1>0)的图象经过点C(-3,0),且与两坐标轴围成的三角形的面积为3.