题目内容
18. 郑州市北环彩虹桥在上下班高峰期经常堵车,交通管理部门为了解交通拥堵情况,进行了统计分析,桥上的车流速度v(km/h)关于车流密度x(辆/km)的函数图象如图所示.
郑州市北环彩虹桥在上下班高峰期经常堵车,交通管理部门为了解交通拥堵情况,进行了统计分析,桥上的车流速度v(km/h)关于车流密度x(辆/km)的函数图象如图所示.(1)请直接写出v与x之间的函数关系式;
(2)在交通高峰时段,为使大桥上的车流速度大于30km/h且小于50km/h,应控制大桥上的车流密度在什么范围内?
(3)车流量y(辆/h)是单位时间内通过桥上某观测点的车辆数,即车流量=车流速度×车流密度,求大桥上车流量的最大值.
分析 (1)直接利用待定系数法求一次函数解析式进而得出答案;
(2)由题知:30<-$\frac{1}{2}$x+90<50时,解不等式组即可得到结论;
(3)根据题意得:y=vx=(-$\frac{1}{2}$x+90)x=-$\frac{1}{2}$x2+90x,化成顶点式y=-$\frac{1}{2}$(x-90)2+8100,即可得到结论.
解答 解:(1)当0<x<20时,v=80,
当20≤x<180时,
设一次函数表达式是V=kx+b,
把两点坐标(20,80)(180,0)分别代入,得 $\left\{\begin{array}{l}{20k+b=80}\\{180k+b=0}\end{array}\right.$,
$\left\{\begin{array}{l}{20k+b=80}\\{180k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=90}\\{\;}\end{array}\right.$,
故V关于x的一次函数表达式是v=-$\frac{1}{2}$x+90;
(2)由题知:30<-$\frac{1}{2}$x+90<50时,
解得:80<x<120.
即车流速度大于30km/h且小于50km/h时,大桥上的车流密度应控制在大于80辆/km<x<120辆/km;
(3)根据题意得:y=vx=(-$\frac{1}{2}$x+90)x=-$\frac{1}{2}$x2+90x,
即y=-$\frac{1}{2}$(x-90)2+8100,
故大桥上车流量的最大值是8100辆/h.
点评 此题主要考查了一次函数和二次函数的应用以及函数最值求法,得出P与x的函数关系式是解题关键.

练习册系列答案
相关题目
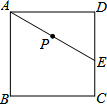 如图,E为正方形ABCD中CD边上一点,∠DAE=30°,P为AE的中点,过点P作直线分别与AD、BC相交于点M、N.若MN=AE,则∠AMN等于60°或120°.
如图,E为正方形ABCD中CD边上一点,∠DAE=30°,P为AE的中点,过点P作直线分别与AD、BC相交于点M、N.若MN=AE,则∠AMN等于60°或120°.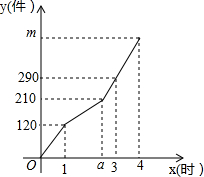 某工厂甲、乙两个车间同时开始生产某种产品,产品总任务量为m件,开始甲、乙两个车间工作效率相同.乙车间在生产一段时间后,停止生产,更换新设备,之后工作效率提高.甲车间始终按原工作效率生产.甲、乙两车间生产的产品总件数y与甲的生产时间x(时)的函数图象如图所示.
某工厂甲、乙两个车间同时开始生产某种产品,产品总任务量为m件,开始甲、乙两个车间工作效率相同.乙车间在生产一段时间后,停止生产,更换新设备,之后工作效率提高.甲车间始终按原工作效率生产.甲、乙两车间生产的产品总件数y与甲的生产时间x(时)的函数图象如图所示.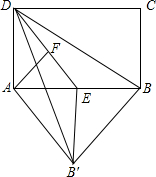 在矩形ABCD中,E为AB边上的中点,将△BDE翻折,B的对应点记为B′,已知AD=4,AB=6,F为线段DE上一动点,当∠DAF=∠BAB′时,则DF+BB′=8.
在矩形ABCD中,E为AB边上的中点,将△BDE翻折,B的对应点记为B′,已知AD=4,AB=6,F为线段DE上一动点,当∠DAF=∠BAB′时,则DF+BB′=8.