题目内容
13.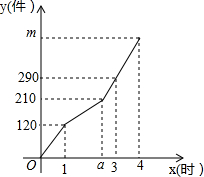 某工厂甲、乙两个车间同时开始生产某种产品,产品总任务量为m件,开始甲、乙两个车间工作效率相同.乙车间在生产一段时间后,停止生产,更换新设备,之后工作效率提高.甲车间始终按原工作效率生产.甲、乙两车间生产的产品总件数y与甲的生产时间x(时)的函数图象如图所示.
某工厂甲、乙两个车间同时开始生产某种产品,产品总任务量为m件,开始甲、乙两个车间工作效率相同.乙车间在生产一段时间后,停止生产,更换新设备,之后工作效率提高.甲车间始终按原工作效率生产.甲、乙两车间生产的产品总件数y与甲的生产时间x(时)的函数图象如图所示.(1)甲车间每小时生产产品60件,a=$\frac{5}{2}$小时.
(2)求乙车间更换新设备之后y与x之间的函数关系式,并求m的值.
(3)若乙车间在开始更换新设备时,增加两名工作人员,这样可便更换设备时间减少0.5小时,并且更换后工作效率提高到原来的2倍,那么两个车间完成原任务量需几小时?
分析 (1)由开始甲、乙两个车间工作效率相同,于是得到开始甲、乙两个车间工作效率是每小时生产产品60个,即可得到结论;
(2)设乙车间更换新设备之后y与x之间的函数关系式为:y=kx+b,把($\frac{5}{2}$,210),(3,290)代入y=kx+b列方程组即可得到结论;
(3)根据两个车间完成原任务量需要的时间=乙车间更换新设备前的时间+乙车间更换新设备中的时间+乙车间更换新设备后的时间,即可得到结论.
解答 解:(1) ∵开始甲、乙两个车间工作效率相同,
∵开始甲、乙两个车间工作效率相同,
∴开始甲、乙两个车间工作效率是每小时生产产品60个,
∴a=$\frac{210-120}{60}$+1=$\frac{5}{2}$小时,
故答案为:60,$\frac{5}{2}$小时;
(2)设乙车间更换新设备之后y与x之间的函数关系式为:y=kx+b,
把($\frac{5}{2}$,210),(3,290)代入y=kx+b得:$\left\{\begin{array}{l}{210=\frac{5}{2}k+b}\\{290=3k+b}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=160}\\{b=-190}\end{array}\right.$,
∴乙车间更换新设备之后y与x之间的函数关系式为:y=160x-190,
当x=4时,y=450,
∴m=450件;
(3)两个车间完成原任务量需要的时间=乙车间更换新设备前的时间+乙车间更换新设备中的时间+乙车间更换新设备后的时间,
即1+($\frac{5}{2}$-1-$\frac{1}{2}$)-[$\frac{450-120-60(\frac{5}{2}-1-\frac{1}{2})}{120+60}$]=$\frac{7}{2}$.
答:两个车间完成原任务量需要的时间是$\frac{7}{2}$小时.
点评 本题考查了一次函数的应用,待定系数法求函数的解析式,正确的识别图象是解题的关键.

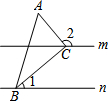 如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且∠ACB=90°,若∠1=40°,则∠2的度数为( )
如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且∠ACB=90°,若∠1=40°,则∠2的度数为( )| A. | 140° | B. | 130° | C. | 120° | D. | 110° |
| A. | a2+a3=a5 | B. | 4a+2b=6ab | C. | ${(\frac{1}{{{a^2}+1}})^0}=1$ | D. | ${(2\sqrt{5})^2}=10$ |
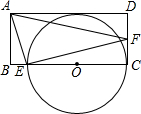 如图,矩形ABCD中,E为BC上一点,F为CD上一点,∠AEF=90°,以EC为直径的⊙O与AD相切,则tan∠AFE的值为( )
如图,矩形ABCD中,E为BC上一点,F为CD上一点,∠AEF=90°,以EC为直径的⊙O与AD相切,则tan∠AFE的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
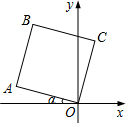 将边长为2的正方形OABC如图放置,O为原点.若∠α=15°,则点B的坐标为(-$\sqrt{2}$,$\sqrt{6}$).
将边长为2的正方形OABC如图放置,O为原点.若∠α=15°,则点B的坐标为(-$\sqrt{2}$,$\sqrt{6}$). 郑州市北环彩虹桥在上下班高峰期经常堵车,交通管理部门为了解交通拥堵情况,进行了统计分析,桥上的车流速度v(km/h)关于车流密度x(辆/km)的函数图象如图所示.
郑州市北环彩虹桥在上下班高峰期经常堵车,交通管理部门为了解交通拥堵情况,进行了统计分析,桥上的车流速度v(km/h)关于车流密度x(辆/km)的函数图象如图所示.