题目内容
8.平面直角坐标系中,存在点A(2,2),B(-6,-4),C(2,-4).则△ABC的外接圆的圆心坐标为(-2,-1),△ABC的外接圆在x轴上所截的弦长为4$\sqrt{6}$.分析 根据三角形的外心是三角形三边垂直平分线的交点解答;连接OM,作MN⊥DE于N,根据勾股定理求出DN,根据垂径定理求出DE.
解答 解:∵B(-6,-4),C(2,-4),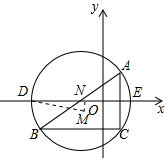
∴线段BC的垂直平分线是x=-2,
∵A(2,2),C(2,-4),
∴线段AC的垂直平分线是y=-1,
∴△ABC的外接圆的圆心M的坐标为:(-2,-1);
连接DM,作MN⊥DE于N,
由题意得,AC=6,BC=8,
由勾股定理得,AB=10,
则DN=$\sqrt{M{D}^{2}-M{N}^{2}}$=2$\sqrt{6}$,
∴DE=4$\sqrt{6}$,
故答案为:(-2,-1);4$\sqrt{6}$.
点评 本题考查的是三角形的外接圆和外心,掌握三角形的外心的概念、垂径定理的应用是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.若函数y=x2m+1为反比例函数,则m的值是( )
| A. | 1 | B. | 0 | C. | 0.5 | D. | -1 |
3.一元二次方程x2-4x+5=0的根的情况是( )
| A. | 没有实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 无法确定 |
20.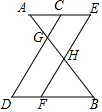 如图,AE∥BD,点C,F分别在线段AE,BD上,连接CD,FE,分别与AB相交于点G、H,若CD∥EF,则下列结论一定正确的是( )
如图,AE∥BD,点C,F分别在线段AE,BD上,连接CD,FE,分别与AB相交于点G、H,若CD∥EF,则下列结论一定正确的是( )
 如图,AE∥BD,点C,F分别在线段AE,BD上,连接CD,FE,分别与AB相交于点G、H,若CD∥EF,则下列结论一定正确的是( )
如图,AE∥BD,点C,F分别在线段AE,BD上,连接CD,FE,分别与AB相交于点G、H,若CD∥EF,则下列结论一定正确的是( )| A. | $\frac{CG}{CD}$=$\frac{EH}{HF}$ | B. | $\frac{AG}{GB}$=$\frac{AC}{CD}$ | C. | $\frac{CE}{GH}$=$\frac{DF}{BG}$ | D. | $\frac{GC}{HE}$=$\frac{AC}{AE}$ |
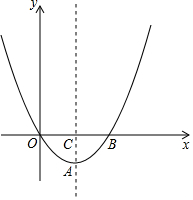 如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2-4ax(a≠0)的对称轴交抛物线于A点,交x轴于C点,且AC=OC.
如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2-4ax(a≠0)的对称轴交抛物线于A点,交x轴于C点,且AC=OC. 如图,C,D是以线段AB为直径的⊙O上的两点,若CA=CD,且∠ACD=40°,则∠CAB的度数为20°.
如图,C,D是以线段AB为直径的⊙O上的两点,若CA=CD,且∠ACD=40°,则∠CAB的度数为20°.