题目内容
5．一个不透明的袋子中装着分别标有数字-3，0，2，4的四个小球，这些小球除标有的数字不同外无其他差别，从袋子中随机摸出一个小球后，放回并摇匀，再随机摸出一个小球，则两次摸出的小球上的数字之和为负数的概率为$\frac{1}{4}$．分析 画树状图列出所有等可能结果，再根据概率公式计算即可得．
解答 解：画树状图如下：
由树状图可知一共有16种等可能结果，其中数字之和为负数有4种等可能结果，
∴两次摸出的小球上的数字之和为负数的概率为$\frac{4}{16}$=$\frac{1}{4}$，
故答案为：$\frac{1}{4}$．
点评 本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果n，再从中选出符合事件A或B的结果数目m，然后利用概率公式计算事件A或事件B的概率．
练习册系列答案
相关题目
15．
如图，AB∥CD，EF⊥BD，垂足为E，∠2=40°，则∠1的度数为（ ）
如图，AB∥CD，EF⊥BD，垂足为E，∠2=40°，则∠1的度数为（ ）| A． | 50° | B． | 40° | C． | 45° | D． | 25° |
16．若函数y=x2m+1为反比例函数，则m的值是（ ）
| A． | 1 | B． | 0 | C． | 0.5 | D． | -1 |
如图，C，D是以线段AB为直径的⊙O上的两点，若CA=CD，且∠ACD=40°，则∠CAB的度数为20°．
20．
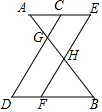如图，AE∥BD，点C，F分别在线段AE，BD上，连接CD，FE，分别与AB相交于点G、H，若CD∥EF，则下列结论一定正确的是（ ）
如图，AE∥BD，点C，F分别在线段AE，BD上，连接CD，FE，分别与AB相交于点G、H，若CD∥EF，则下列结论一定正确的是（ ）| A． | $\frac{CG}{CD}$=$\frac{EH}{HF}$ | B． | $\frac{AG}{GB}$=$\frac{AC}{CD}$ | C． | $\frac{CE}{GH}$=$\frac{DF}{BG}$ | D． | $\frac{GC}{HE}$=$\frac{AC}{AE}$ |