题目内容
17.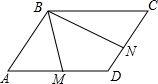 在?ABCD中,M是AD的中点,N是DC的中点,BM=1,BN=2,∠MBN=60°,求BC的长.
在?ABCD中,M是AD的中点,N是DC的中点,BM=1,BN=2,∠MBN=60°,求BC的长.
分析 如图延长DM交CB的延长线于H,作MK⊥AD于K,先证明△AMB≌△DMH,得BH=BN,△HBN是等边三角形,可以求出AB=DH=$\frac{4}{3}$,在RT△BNK和RT△AKM中利用勾股定理即可解决.
解答 解:如图延长DM交CB的延长线于H,作MK⊥AD于K.
∵四边形ABCD是平行四边形,
∴AD∥BC,CD∥AB,AD=BC,AB=CD,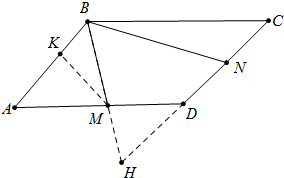
∴∠A=∠HDM,
在△AMD和△BMH中,
$\left\{\begin{array}{l}{∠A=∠HDM}\\{AM=DM}\\{∠AMB=∠HMD}\end{array}\right.$,
∴△AMB≌△DMH,
∴AB=DH,BM=MH=2,
∵BN=2,∠HBN=60°,
∴BH=BN,
∴△BHN是等边三角形,
∴HN=2,∵BN=NC=$\frac{1}{2}$CD=$\frac{1}{2}$AB=$\frac{1}{2}$NH,∠H=∠ABM=60°,
∴AB=DH=$\frac{4}{3}$,
在RT△MKB中,∵∠MKB=90°,MB=1,∠MBK=60°,
∴BK=$\frac{1}{2}$BM=$\frac{1}{2}$,KM=$\sqrt{3}$BK=$\frac{\sqrt{3}}{2}$,AK=AB-BK=$\frac{5}{6}$,
∴AM=$\sqrt{A{K}^{2}+K{M}^{2}}$=$\sqrt{(\frac{5}{6})^{2}+(\frac{\sqrt{3}}{2})^{2}}$=$\frac{\sqrt{13}}{3}$,
∴BC=AD=2AM=$\frac{\sqrt{13}}{3}$.
点评 本题考查平行四边形的性质、全等三角形的判定和性质、等边三角形的判定和性质、勾股定理等知识,解题的关键是添加辅助线构造全等三角形,得出△BNH是等边三角形这个突破口,属于中考常考题型.

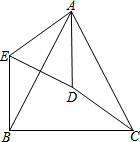 如图,在△ABC中,AB=AC,D是△ABC的外心,连接AD、CD.将△ADC绕点A顺时针旋转到△AEB,连接ED.
如图,在△ABC中,AB=AC,D是△ABC的外心,连接AD、CD.将△ADC绕点A顺时针旋转到△AEB,连接ED.(1)求证:△AED∽△ABC;
(2)连接BD,判断四边形AEBD的形状并证明.
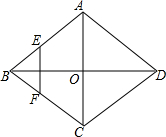 如图,菱形ABCD的对角线AC、BD相交于点O,E、F分别是AB、BC边的中点,连接EF,若EF=$\sqrt{3}$,BD=4,则菱形ABCD的边长为( )
如图,菱形ABCD的对角线AC、BD相交于点O,E、F分别是AB、BC边的中点,连接EF,若EF=$\sqrt{3}$,BD=4,则菱形ABCD的边长为( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $\sqrt{7}$ | D. | 7 |
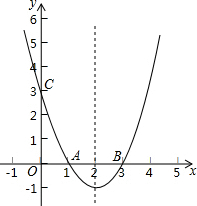 已知二次函数y=ax2+bx+c的图象交x轴于A(1,0)和B(3,0),交y轴于C(0,3),P是对称轴上的动点,求△PAC周长的最小值.
已知二次函数y=ax2+bx+c的图象交x轴于A(1,0)和B(3,0),交y轴于C(0,3),P是对称轴上的动点,求△PAC周长的最小值.
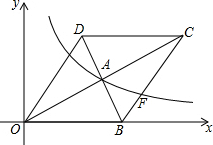 如图,在平面直角坐标系中.菱形OBCD的边OB在x轴正半轴上,反比例函数y=$\frac{k}{x}$的图象经过该菱形对角线的交点A,且与边BC交于点F,若点D的坐标为(6,8),求点F的坐标.
如图,在平面直角坐标系中.菱形OBCD的边OB在x轴正半轴上,反比例函数y=$\frac{k}{x}$的图象经过该菱形对角线的交点A,且与边BC交于点F,若点D的坐标为(6,8),求点F的坐标.