题目内容
8.己知反比例函数y=$\frac{k-1}{x}$(k常数,k≠1).(1)若点A(2,1)在这个函数的图象上,求k的值;
(2)若在这个函数图象的每一个分支上,y随x的增大而增大,求k的取值范围;
(3)若k=9,试判断点B(-$\frac{1}{2}$,-16)是否在这个函数的图象上,并说明理由.
分析 (1)根据反比例函数图象上点的坐标特征得到k-1=2×1,然后解方程即可;
(2)根据反比例函数的性质得k-1<0,然后解不等式;
(3)根据反比例好图象上点的坐标特征解析判断.
解答 解:(1)把A(2,1)代入y=$\frac{k-1}{x}$得k-1=2×1,解得k=3;
(2)根据题意得k-1<0,解得k<1;
(3)在.理由如下:
当k=9时,反比例函数解析式为y=$\frac{8}{x}$,
因为-$\frac{1}{2}$×(-16)=8,
所以点B在这个函数的图象上.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了反比例函数的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列图形中,是中心对称图形但不是轴对称图形的是( )
| A. | 等边三角形 | B. | 圆 | C. | 矩形 | D. | 平行四边形 |
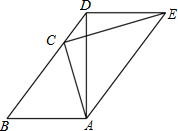 如图,在△ABC中,AB=AC,作AD⊥AB交BC的延长线于点D,作CE⊥AC,且使AE∥BD,连结DE.
如图,在△ABC中,AB=AC,作AD⊥AB交BC的延长线于点D,作CE⊥AC,且使AE∥BD,连结DE. 如图,矩形ABCD中,点E、F分别是AB、CD边上的点,且AE=CF,点G、H分别为DE和BF的中点,求证:AG=CH.
如图,矩形ABCD中,点E、F分别是AB、CD边上的点,且AE=CF,点G、H分别为DE和BF的中点,求证:AG=CH.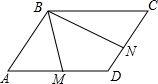 在?ABCD中,M是AD的中点,N是DC的中点,BM=1,BN=2,∠MBN=60°,求BC的长.
在?ABCD中,M是AD的中点,N是DC的中点,BM=1,BN=2,∠MBN=60°,求BC的长.