题目内容
2.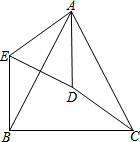 如图,在△ABC中,AB=AC,D是△ABC的外心,连接AD、CD.将△ADC绕点A顺时针旋转到△AEB,连接ED.
如图,在△ABC中,AB=AC,D是△ABC的外心,连接AD、CD.将△ADC绕点A顺时针旋转到△AEB,连接ED.(1)求证:△AED∽△ABC;
(2)连接BD,判断四边形AEBD的形状并证明.
分析 (1)由旋转性质可得∠DAE=∠CAB、AE=AD,结合AB=AC根据$\frac{AE}{AB}$=$\frac{AD}{AC}$且∠DAE=∠CAB可证得;
(2)由三角形外心可得DB=DA=DC,结合△ADC≌△AEB知DB=DA=BE=AE,即可判定四边形AEBD的形状.
解答 证明:(1)∵△ADC 绕点A顺时针旋转得到△AEB,
∴△ADC≌△AEB.
∴∠BAE=∠CAD,AE=AD.
∴∠DAE=∠CAB.
∵AB=AC,
∴$\frac{AE}{AB}$=$\frac{AD}{AC}$.
∴△AED∽△ABC.
(2)四边形AEBD是菱形.
∵D是△ABC的外心,
∴DB=DA=DC.
又∵△ADC≌△AEB,
∴AE=AD,BE=DC.
∴DB=DA=BE=AE.
∴四边形AEBD是菱形.
点评 本题主要考查相似三角形的判定及菱形的判定,熟练掌握旋转的性质及三角形外心的性质是解题的关键.

练习册系列答案
相关题目
12.下列方程组中,属于二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{x+y=5}\\{\frac{1}{x}+\frac{1}{y}=\frac{5}{6}}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{{x}^{2}+y=10}\\{x+y=-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=8}\\{xy=-5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{x+y=-3}\end{array}\right.$ |
 如图,矩形ABCD中,点E、F分别是AB、CD边上的点,且AE=CF,点G、H分别为DE和BF的中点,求证:AG=CH.
如图,矩形ABCD中,点E、F分别是AB、CD边上的点,且AE=CF,点G、H分别为DE和BF的中点,求证:AG=CH.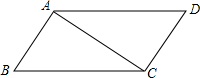 已平行四边形ABCD中∠B=55°,∠2=35°,AD=10,对角线AC=8,求平行四边形ABCD各内角的度数及各边的长.
已平行四边形ABCD中∠B=55°,∠2=35°,AD=10,对角线AC=8,求平行四边形ABCD各内角的度数及各边的长.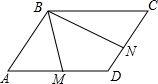 在?ABCD中,M是AD的中点,N是DC的中点,BM=1,BN=2,∠MBN=60°,求BC的长.
在?ABCD中,M是AD的中点,N是DC的中点,BM=1,BN=2,∠MBN=60°,求BC的长.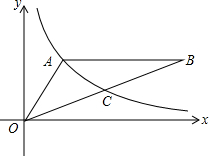 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3).
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3).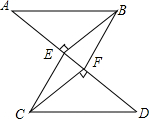 如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.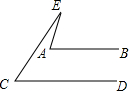 如图,AB∥CD,∠EAB=75°,∠C=51°,则∠E=24°.
如图,AB∥CD,∠EAB=75°,∠C=51°,则∠E=24°.