题目内容
11.某商场准备购进两种型号的摩托车共25辆,预计投资10万元.现有甲、乙、丙三种摩托车,甲种每辆4200元,可获利400元;乙种每辆3700元,可获利350元;丙种每辆3100元,可获利300元.10万元资本全部用完.(1)请你帮助该商场设计进货方案;
(2)从销售利润上考虑,应选择哪种方案?
分析 (1)分当购进甲、乙两种型号的摩托车;购进甲、丙两种型号的摩托车;购进乙、丙两种型号的摩托车三种情况.并分别通过设出未知数,解二元一次方程组来解答.
(2)根据(1)的结论求出每种近货方案的利润,选择利润最大的那种方案就可以了.
解答 解:(1)设购进甲种x辆,乙种y辆,则
$\left\{\begin{array}{l}{x+y=25}\\{4200x+3700y=100000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=15}\\{y=10}\end{array}\right.$,
设购进甲种m辆,丙种n辆,则
$\left\{\begin{array}{l}{m+n=25}\\{4200m+3100n=100000}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=20\\}\\{n=5}\end{array}\right.$,
设购进乙种a辆,丙种b辆,则
$\left\{\begin{array}{l}{a+b=25}\\{3700a+3100b=100000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=40}\\{b=-15}\end{array}\right.$(不符合题意,舍去)
故进货方案有两种:①甲种进15辆,乙种进10辆;②甲种进20辆,乙种进5辆.
(2)由(1)得,方案1的销售利润为:
400×15+350×10=9500元;
方案2的销售利润为:
400×20+320×5=9600.
∵9600>9500.
∴从销售利润上看要选择方案2.
点评 本题考查了运用二元一次方程组解决实际问题的运用,方程组的解法及实数大小的比较的运用,在方案设计中全面考虑问题是很关键的.

 阅读快车系列答案
阅读快车系列答案| A. | 五边形 | B. | 四边形 | C. | 六边形 | D. | 七边形 |
| A. | $\frac{2+x}{x}$ | B. | $\frac{{x}^{2}+1}{2x}$ | C. | $\frac{1}{{x}^{2}}$ | D. | $\frac{2x-1}{{x}^{2}+1}$ |
 如图,D、E、F在同一条直线上,A、B、C在同一条直线上,∠C=∠D,∠D+∠DEC=180°,求证:AC∥DF,DB∥EC.
如图,D、E、F在同一条直线上,A、B、C在同一条直线上,∠C=∠D,∠D+∠DEC=180°,求证:AC∥DF,DB∥EC.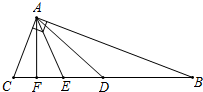 如图,在△ABC中,∠BAC=90°,∠B<22.5°,AD、AE、AF分别是中线、角平分线、高,如果把图中相等的锐角都记为一组,则共有( )
如图,在△ABC中,∠BAC=90°,∠B<22.5°,AD、AE、AF分别是中线、角平分线、高,如果把图中相等的锐角都记为一组,则共有( )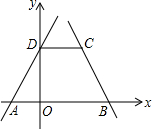 一次函数y=2x+2图象与x轴、y轴分别交于A、D两点,一次函数y=-2x+8与x轴交于B点,过D点作DC∥x轴,交直线y=-2x+8于点C.
一次函数y=2x+2图象与x轴、y轴分别交于A、D两点,一次函数y=-2x+8与x轴交于B点,过D点作DC∥x轴,交直线y=-2x+8于点C.