题目内容
6．已知多边形的内角和与某一个内角的度数总和为2190°，求这个角的边数．分析 根据n边形的内角和定理可知：n边形内角和为（n-2）×180°．设这个内角度数为x度，利用方程即可求出答案．
解答 解：设这个内角度数为x，根据题意，得
（n-2）×180°+x=2190°，
解得：x=2190°-180°n+360°=2550°-180°n，
由于0＜x＜180°，即0＜2550°-180°n＜180°，
解得13.5＜n＜14.5，
所以n=14．
故多边形的边数是14
点评 主要考查了多边形的内角和定理．n边形的内角和为：180°•（n-2）．
练习册系列答案
相关题目
如图，在平行四边形ABCD中，E是AD边上的中点，连接BE，并延长BE交CD的延长线于点F．证明：FD=AB．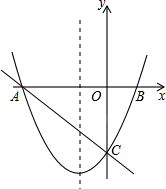
如图，在直角坐标系xOy中，一次函数y=-$\frac{2}{3}$x+m（m为常数）的图象与x轴交于A（-3，0），与y轴交于点C．以直线x=-1为对称轴的抛物线y=ax2+bx+c（a，b，c为常数，且a＞0）经过A、C两点，与x轴正半轴交于点B．
14．下列关于y与x的表达式中，反映y是x的反比例函数的是（ ）
| A． | y=4x | B． | $\frac{x}{y}$=-2 | C． | xy=4 | D． | y=4x-3 |
已知：等边△ABC，边长为8cm，点D从C点出发沿BC方向以1cm/s速度运动，点P从A点出发沿AC方向以2cm/s速度运动，DE∥AC交AB于点E，点D、点P两点同时出发，设运动时间为t s，问：