题目内容
6.现一个圆心角为120°,半径为6cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),该圆锥底面圆的面积为( )| A. | 4πcm2 | B. | 9πcm2 | C. | 16πcm2 | D. | πcm2 |
分析 利用扇形弧长等积式公式求出扇形的弧长,根据扇形的弧长等于它围成的圆锥的底面周长解得即可.
解答 解:∵扇形纸片的圆心角为120°,半径为6cm,
∴扇形纸片的弧长为$\frac{120π×6}{180}$=4π,
∴圆锥的底面周长为4π,
则圆锥的底面半径为2,
该圆锥底面圆的面积为4πcm2,
故选:A.
点评 本题考查的是圆锥的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
14. 如图,AB是⊙O的直径,点C、D在⊙O上,∠AOC=40°,AC∥OD,则的∠BOD度数( )
如图,AB是⊙O的直径,点C、D在⊙O上,∠AOC=40°,AC∥OD,则的∠BOD度数( )
 如图,AB是⊙O的直径,点C、D在⊙O上,∠AOC=40°,AC∥OD,则的∠BOD度数( )
如图,AB是⊙O的直径,点C、D在⊙O上,∠AOC=40°,AC∥OD,则的∠BOD度数( )| A. | 140° | B. | 130° | C. | 120° | D. | 110° |
11.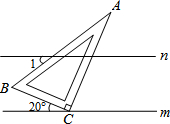 已知:如图,直线m∥n,一把直角三角板ABC(其中∠A=30°)的直角顶点C放在直线m上,边BC与直线m所夹锐角为20°,则∠1的度数为( )
已知:如图,直线m∥n,一把直角三角板ABC(其中∠A=30°)的直角顶点C放在直线m上,边BC与直线m所夹锐角为20°,则∠1的度数为( )
 已知:如图,直线m∥n,一把直角三角板ABC(其中∠A=30°)的直角顶点C放在直线m上,边BC与直线m所夹锐角为20°,则∠1的度数为( )
已知:如图,直线m∥n,一把直角三角板ABC(其中∠A=30°)的直角顶点C放在直线m上,边BC与直线m所夹锐角为20°,则∠1的度数为( )| A. | 30° | B. | 40° | C. | 45° | D. | 60° |
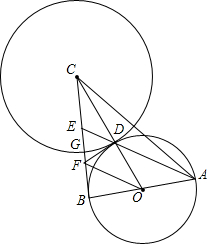 如图:Rt△ABC中,∠ABC=90°,AB=BC,以AB为直径的⊙O交OC于D,AD的延长线交BC于E,过点D作⊙O的切线DF交BC于F,连接OF.⊙C切⊙O于点D,交BC于G
如图:Rt△ABC中,∠ABC=90°,AB=BC,以AB为直径的⊙O交OC于D,AD的延长线交BC于E,过点D作⊙O的切线DF交BC于F,连接OF.⊙C切⊙O于点D,交BC于G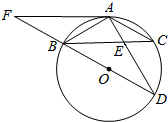 如图,BD为⊙O的直径,AB=AC,AD交BC于点E,延长DB交⊙O的切线AF于点F,AE=2,ED=4.
如图,BD为⊙O的直径,AB=AC,AD交BC于点E,延长DB交⊙O的切线AF于点F,AE=2,ED=4.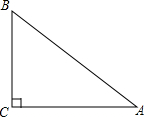 如图,△ABC中,∠C=90°.
如图,△ABC中,∠C=90°.