题目内容
11.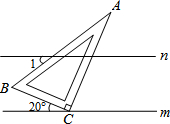 已知:如图,直线m∥n,一把直角三角板ABC(其中∠A=30°)的直角顶点C放在直线m上,边BC与直线m所夹锐角为20°,则∠1的度数为( )
已知:如图,直线m∥n,一把直角三角板ABC(其中∠A=30°)的直角顶点C放在直线m上,边BC与直线m所夹锐角为20°,则∠1的度数为( )| A. | 30° | B. | 40° | C. | 45° | D. | 60° |
分析 作BD∥m交AC于D,由平行线的性质得出∠DBC=∠BCE=20°,由直角三角形的性质得出∠ABC=60°,求出∠ABD=40°,由平行线的性质得出∠1=∠ABD=40°即可.
解答 解:作BD∥m交AC于D,如图所示:
则∠DBC=∠BCE=20°,
∵∠ACB=90°,∠A=30°,
∴∠ABC=90°-30°=60°,
∴∠ABD=60°-20°=40°,
∵m∥n,BD∥m,
∴BD∥n,
∴∠1=∠ABD=40°;
故选:B.
点评 本题考查了平行线的性质、直角三角形的性质;熟练掌握平行线的性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
相关题目
6.现一个圆心角为120°,半径为6cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),该圆锥底面圆的面积为( )
| A. | 4πcm2 | B. | 9πcm2 | C. | 16πcm2 | D. | πcm2 |
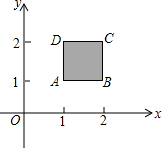 如图,在平面直角坐标系内有一正方形ABCD,其项点坐标分别为A(1,1),B(2,1),C(2,2),D(1,2),要使直线y=-2x+b和此正方形有交点的b的取值范围为3≤x≤6.
如图,在平面直角坐标系内有一正方形ABCD,其项点坐标分别为A(1,1),B(2,1),C(2,2),D(1,2),要使直线y=-2x+b和此正方形有交点的b的取值范围为3≤x≤6. 笑脸(2)是由笑脸(1)经过旋转变换得到的.
笑脸(2)是由笑脸(1)经过旋转变换得到的.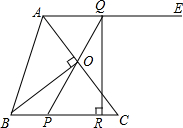 如图,在△ABC中,AB=BC=10,AC=12,BO⊥AC,垂足为点O,过点A作射线AE∥BC,点P是边BC上任意一点(可与B、C重合),连接PO并延长与射线AE相交于点Q,过点Q作直线BC的垂线,垂足为R.设B,P两点之间的距离为x,当x=$\frac{14}{5}$时,△PQR∽△ABO成立.
如图,在△ABC中,AB=BC=10,AC=12,BO⊥AC,垂足为点O,过点A作射线AE∥BC,点P是边BC上任意一点(可与B、C重合),连接PO并延长与射线AE相交于点Q,过点Q作直线BC的垂线,垂足为R.设B,P两点之间的距离为x,当x=$\frac{14}{5}$时,△PQR∽△ABO成立. 如图,梯形ABCD是拦水坝的横断面图(图中i=$1:\sqrt{3}$是指坡面的垂直高度DE与水平宽度CE的比)∠B=60°,AB=6cm,AD=5cm,求拦水坝的横断面ABCD的面积(结果保留三位有效数字,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
如图,梯形ABCD是拦水坝的横断面图(图中i=$1:\sqrt{3}$是指坡面的垂直高度DE与水平宽度CE的比)∠B=60°,AB=6cm,AD=5cm,求拦水坝的横断面ABCD的面积(结果保留三位有效数字,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)