题目内容
16.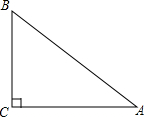 如图,△ABC中,∠C=90°.
如图,△ABC中,∠C=90°.(1)将△ABC绕点B逆时针旋转90°,画出旋转后的三角形;
(2)若BC=3,AC=4.点A旋转后的对应点为A′,求A′A的长.
分析 (1)利用旋转的性质画出点A和点C的对应点A′、C′即可得到△BA′C′;
(2)先利用勾股定理计算出AB=5,再利用旋转的性质得BA′=BA=5,∠A′BA=90°,则可判断△A′BA为等腰直角三角形,然后根据等腰直角三角形的性质求解.
解答 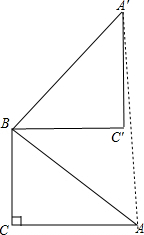 解:(1)如图,△BA′C′为所作;
解:(1)如图,△BA′C′为所作;
(2)△ABC中,∵∠C=90°,BC=3,AC=4,
∴AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵△ABC绕点B逆时针旋转90°得到△BA′C′,
∴BA′=BA=5,∠A′BA=90°,
∴△A′BA为等腰直角三角形,
∴A′A=$\sqrt{2}$BA=5$\sqrt{2}$.
点评 本题考查了作图:旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.

练习册系列答案
相关题目
6.现一个圆心角为120°,半径为6cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),该圆锥底面圆的面积为( )
| A. | 4πcm2 | B. | 9πcm2 | C. | 16πcm2 | D. | πcm2 |
7.下列图形中,有且只有两条对称轴的图形是( )
| A. | 点 | B. | 线段 | C. | 射线 | D. | 直线 |
8.用科学记数法表示290000 0000为( )
| A. | 0.29×1010 | B. | 2.9×109 | C. | 29×108 | D. | 2.9×108 |
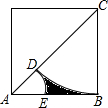 如图,正方形ABCD的边长为2,以CB为半径的弧交AC于D,以AD为半径的弧交AB于E,则图中阴影部分的面积为2-(2-$\sqrt{2}$)π.
如图,正方形ABCD的边长为2,以CB为半径的弧交AC于D,以AD为半径的弧交AB于E,则图中阴影部分的面积为2-(2-$\sqrt{2}$)π. 如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.
如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.