题目内容
1.观察下列各式及其验证过程:$\sqrt{2+\frac{2}{3}}=2\sqrt{\frac{2}{3}}$,验证:$\sqrt{2+\frac{2}{3}}=\sqrt{\frac{8}{3}}=\sqrt{\frac{{{2^2}×2}}{3}}=2\sqrt{\frac{2}{3}}$.$\sqrt{3+\frac{3}{8}}=3\sqrt{\frac{3}{8}}$,验证:$\sqrt{3+\frac{3}{8}}=\sqrt{\frac{27}{8}}=\sqrt{\frac{{{3^2}×3}}{8}}=3\sqrt{\frac{3}{8}}$.(1)按照上述两个等式及其验证过程,猜想$\sqrt{4+\frac{4}{15}}$的变形结果并进行验证.
(2)针对上述各式反映的规律,写出用a(a为任意自然数,且a≥2)表示的等式,并给出验证.
(3)针对三次根式及n次根式(n为任意自然数,且n≥2),有无上述类似的变形?如果有,写出用a(a为任意自然数,且a≥2)表示的等式,并给出验证.
分析 (1)利用已知,观察$\sqrt{2+\frac{2}{3}}=\sqrt{\frac{8}{3}}=\sqrt{\frac{{{2^2}×2}}{3}}=2\sqrt{\frac{2}{3}}$.$\sqrt{3+\frac{3}{8}}=3\sqrt{\frac{3}{8}}$,可得$\sqrt{4+\frac{4}{15}}$的值;
(2)由(1)根据二次根式的性质可以总结出一般规律;
(3)利用已知可得出三次根式的类似规律,进而验证即可.
解答 解:(1)$\sqrt{4+\frac{4}{15}}$=4$\sqrt{\frac{4}{15}}$,
理由是:$\sqrt{4+\frac{4}{15}}$=$\sqrt{\frac{64}{15}}$=$\sqrt{\frac{{4}^{2}×4}{15}}$=4$\sqrt{\frac{4}{15}}$;
(2)由(1)中的规律可知3=22-1,8=32-1,15=42-1,
∴$\sqrt{a+\frac{a}{{a}^{2}-1}}$=a$\sqrt{\frac{a}{{a}^{2}-1}}$,
验证:$\sqrt{a+\frac{a}{{a}^{2}-1}}$=$\sqrt{\frac{{a}^{3}}{{a}^{2}-1}}$=a$\sqrt{\frac{a}{{a}^{2}-1}}$;正确;
(3)$\root{3}{a+\frac{1}{{a}^{3}-1}}$=a$\root{3}{\frac{a}{{a}^{3}-1}}$(a为任意自然数,且a≥2),
验证:$\root{3}{a+\frac{1}{{a}^{3}-1}}$=$\root{3}{\frac{{a}^{4}-a+a}{{a}^{3}-1}}$=$\root{3}{\frac{{a}^{4}}{{a}^{3}-1}}$=a$\root{3}{\frac{a}{{a}^{3}-1}}$.
点评 此题主要考查二次根式的性质与化简,善于发现题目数字之间的规律,是解题的关键.

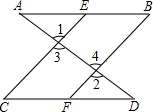 如图,已知AD与AB,CD交于A,D两点,EC,BF与AB,CD交于E,C,B,F,且∠1=∠2,∠B=∠C,说明CE∥BF.
如图,已知AD与AB,CD交于A,D两点,EC,BF与AB,CD交于E,C,B,F,且∠1=∠2,∠B=∠C,说明CE∥BF.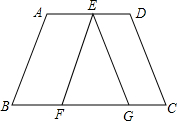 已知:如图,AB∥EF,CD∥EG,AD∥BC,∠A=125°,∠D=95°,求∠EFG、∠EGF、∠GEF的度数.
已知:如图,AB∥EF,CD∥EG,AD∥BC,∠A=125°,∠D=95°,求∠EFG、∠EGF、∠GEF的度数.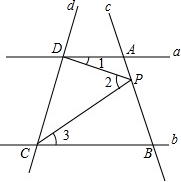 如图,已知直线c和a、b分别交于A、B两点,点P在直线c上运动.
如图,已知直线c和a、b分别交于A、B两点,点P在直线c上运动.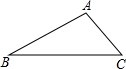 如图,△ABC是一仓库的屋顶的横截面,若∠B=30°,∠C=45°,AC=2,求线段AB的长.
如图,△ABC是一仓库的屋顶的横截面,若∠B=30°,∠C=45°,AC=2,求线段AB的长. 在所建立的平面直角坐标系中:
在所建立的平面直角坐标系中: