题目内容
10.已知反比例函数y=$\frac{4}{x}$的图象上有A(1,m)、B(a,b)、C(n,1)三点,其中1<a<4,则△ABC的最大面积是$\frac{3}{2}$.分析 首先根据反比例函数图象上点的坐标特点求出B、C两点坐标,然后再过A、C作AM⊥CM,再过B作BN⊥CM,△ABC的面积=△AMC的面积-梯形AMNB的面积-△BNC的面积即可.
解答 解:∵反比例函数y=$\frac{4}{x}$的图象上有三点A(1,m)、B(a,b)、C(n,1),
∴m=4,n=4,
∴A(1,4),C(4,1),
∴A、C关于直线y=x对称,
∵1<a<4,
∴当B点是直线y=x和y=$\frac{4}{x}$的交点时,△ABC的面积最大,
∴B(2,2),
过A、C作AM⊥CM,再过B作BN⊥CM,
则△ABC的面积S=$\frac{1}{2}$×AM×CM-$\frac{1}{2}$(AM+BN)×NM-$\frac{1}{2}$BN×CN=$\frac{1}{2}$×3×3-$\frac{1}{2}$(1+3)×1-$\frac{1}{2}$×1×2=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 此题主要考查了反比例函数图象上点的坐标特点,关键是掌握反比例图象上横、纵坐标的积是定值k.

练习册系列答案
相关题目
2.下列各数:①$\frac{22}{7}$;②$\sqrt{3}$;③$-\sqrt{4}$;④π.其中无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
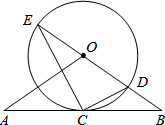 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD.
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD.
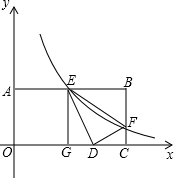 如图,双曲线y=$\frac{k}{x}$与矩形OABC两边AB,BC分别交于E,F.若将三角形BEF沿直线EF对折,点D刚好落在x轴上的D点,其中OA=1,AB=2,则k的值为$\frac{3}{4}$.
如图,双曲线y=$\frac{k}{x}$与矩形OABC两边AB,BC分别交于E,F.若将三角形BEF沿直线EF对折,点D刚好落在x轴上的D点,其中OA=1,AB=2,则k的值为$\frac{3}{4}$.