题目内容

13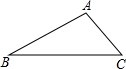．如图，△ABC是一仓库的屋顶的横截面，若∠B=30°，∠C=45°，AC=2，求线段AB的长．

分析 过点A作AD⊥BC，根据题意可以求得AD的值，再根据含30°角直角三角形中斜边长为30°角所对直角边一半，根据勾股定理即可解题．

解答 解：过点A作AD⊥BC，
∵∠C=45°，
∴∠DAC=45°，
∴AD=CD，
∵AD2+CD2=AC2．
∴AD=$\sqrt{2}$，
在Rt△ABD中，AB2=AD2+BD2，
∵∠BAD=30°，
∴AB=2AD，
解得AB=2$\sqrt{2}$．

点评 本题考查了勾股定理的运用，考查了含30°角直角三角形中斜边长为30°角所对直角边一半的性质，考查了等腰直角三角形腰长相等的性质．

练习册系列答案
相关题目
3．已知关于x的不等式2x-a＞2与不等式3x＞4的解集相同，求a的值．
4．若反比例函数y=$\frac{-{k}^{2}-1}{x}$的图象经过点（-2，a），（-1，b），（3，c），则a，b，c的大小关系为c＜a＜b．
1．观察下列各式及其验证过程：$\sqrt{2+\frac{2}{3}}=2\sqrt{\frac{2}{3}}$，验证：$\sqrt{2+\frac{2}{3}}=\sqrt{\frac{8}{3}}=\sqrt{\frac{{{2^2}×2}}{3}}=2\sqrt{\frac{2}{3}}$．$\sqrt{3+\frac{3}{8}}=3\sqrt{\frac{3}{8}}$，验证：$\sqrt{3+\frac{3}{8}}=\sqrt{\frac{27}{8}}=\sqrt{\frac{{{3^2}×3}}{8}}=3\sqrt{\frac{3}{8}}$．
（1）按照上述两个等式及其验证过程，猜想$\sqrt{4+\frac{4}{15}}$的变形结果并进行验证．
（2）针对上述各式反映的规律，写出用a（a为任意自然数，且a≥2）表示的等式，并给出验证．
（3）针对三次根式及n次根式（n为任意自然数，且n≥2），有无上述类似的变形？如果有，写出用a（a为任意自然数，且a≥2）表示的等式，并给出验证．
8．在平面直角坐标系中，O为坐标原点，点A在第四象限，点B在x轴正半轴上，△OAB的面积为6，点P在线段AB上，并把线段分成1：2两部分，若反比例函数y=$\frac{k}{x}$的图象经过点A，P，则k的值为3或-$\frac{24}{5}$．
18．8点55分时，钟表上时针与分针的所成的角是62.5°．
5．若2a-3b=0（b≠0），则$\frac{a}{b}$=$\frac{3}{2}$．
2．下列各数：①$\frac{22}{7}$；②$\sqrt{3}$；③$-\sqrt{4}$；④π．其中无理数有（　　）
A．1个B．2个C．3个D．4个
3．某校九（18）班开展数学活动，毓齐和博文两位同学合作用测角仪测量学校的旗杆，毓齐站在B点测得旗杆顶端E点的仰角为45°，博文站在D（D点在直线FB上）测得旗杆顶端E点仰角为15°，已知毓齐和博文相距（BD）30米，毓齐的身高（AB）1.6米，博文的身高（CD）1.75米，求旗杆的高EF的长．（结果精确到0.1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网