题目内容

6．计算：（9+1）（92+1）（94+1）（98+1）（916+1）（932+1）+$\frac{1}{8}$．

分析 原式变形后，利用平方差公式计算即可得到结果．

解答 解：原式=$\frac{1}{8}$（9-1）（9+1）（92+1）（94+1）（98+1）（916+1）（932+1）+$\frac{1}{8}$
=$\frac{1}{8}$（92-1）（92+1）（94+1）（98+1）（916+1）（932+1）+$\frac{1}{8}$
=$\frac{1}{8}$（94-1）（94+1）（98+1）（916+1）（932+1）+$\frac{1}{8}$
=$\frac{1}{8}$（98-1）（98+1）（916+1）（932+1）+$\frac{1}{8}$
=$\frac{1}{8}$（916-1）（916+1）（932+1）+$\frac{1}{8}$
=$\frac{1}{8}$（932-1）（932+1）+$\frac{1}{8}$
=$\frac{1}{8}$（964-1）+$\frac{1}{8}$
=$\frac{{9}^{64}}{8}$．

点评 此题考查了平方差公式，熟练掌握公式是解本题的关键．

练习册系列答案
相关题目
16．（1）计算：|$\root{3}{27}$|+|-$\sqrt{16}$|+$\sqrt{4}$-$\root{3}{8}$；     
（2）解方程：125（-x+1）3=512．
17．解不等式组：$\left\{\begin{array}{l}{2x-1＞5}\\{\frac{3x+1}{2}-1≥x}\end{array}\right.$．
14．（1）（x-y-z）（x-y+z）；                   
（2）（$\frac{1}{3}$x+y）（-y+$\frac{1}{3}$x）（$\frac{1}{9}$x2-y2）；
（3）化简求值：a2（a+b）（a-b）-（2b-a2）（-2b+a2），其中a=2，b=$\frac{1}{2}$．
1．观察下列各式及其验证过程：$\sqrt{2+\frac{2}{3}}=2\sqrt{\frac{2}{3}}$，验证：$\sqrt{2+\frac{2}{3}}=\sqrt{\frac{8}{3}}=\sqrt{\frac{{{2^2}×2}}{3}}=2\sqrt{\frac{2}{3}}$．$\sqrt{3+\frac{3}{8}}=3\sqrt{\frac{3}{8}}$，验证：$\sqrt{3+\frac{3}{8}}=\sqrt{\frac{27}{8}}=\sqrt{\frac{{{3^2}×3}}{8}}=3\sqrt{\frac{3}{8}}$．
（1）按照上述两个等式及其验证过程，猜想$\sqrt{4+\frac{4}{15}}$的变形结果并进行验证．
（2）针对上述各式反映的规律，写出用a（a为任意自然数，且a≥2）表示的等式，并给出验证．
（3）针对三次根式及n次根式（n为任意自然数，且n≥2），有无上述类似的变形？如果有，写出用a（a为任意自然数，且a≥2）表示的等式，并给出验证．
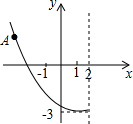11．如图，二次函数y=ax2+bx+c的图象的一部分，已知A（-2.5，2），则根据图象可得到下列结论：
①a＞0，b2-4ac＞0；
②x＜m时，y随x的增大而减小，则m≤2；
③-2.5≤x＜4时，-3≤y≤2；
④-3≤y≤0时，-1≤x≤5．
其中正确的序号是①②③．
18．8点55分时，钟表上时针与分针的所成的角是62.5°．
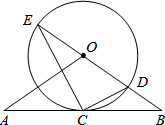15．如图，直线AB经过⊙O上的点C，并且OA=OB，CA=CB，⊙O交直线OB于E，D，连接EC，CD．
（1）求证：直线AB是⊙O的切线；
（2）若tan∠CED=$\frac{1}{2}$，⊙O的半径为3，求OA的长．
16．如果|a+2|+（b-1）2=0，那么代数式（a+b）2014的值是1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网