题目内容
3．
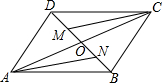如图．在?ABCD中．对角线AC，BD交于点O，M，N分别是OD，OB的中点，连接CM，AN．求证：CM=AN．
分析 根据平行四边形的对角线互相平分以及中点的定义可得OA=OC，OM=ON，然后证明△OAN≌△OCM，根据全等三角形的对应边相等证得．
解答 证明：∵平行四边形ABCD中，OA=OC，OB=OD，
又∵M、N是OD、OB的中点，
∴OM=0N，
∴在△OAN和△OCM中，
$\left\{\begin{array}{l}{OM=ON}\\{∠MOC=∠NOA}\\{OA=OC}\end{array}\right.$，
∴△OAN≌△OCM，
∴CM=AN．
点评 本题考查了平行四边形的性质，对角线互相平分以及全等三角形的判定与性质，正确证明△OAN≌△OCM是关键．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
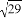时，求t的值；
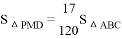？若存在，请求出t的值；若不存在，请说明理由．
B. 
C. 
D. 
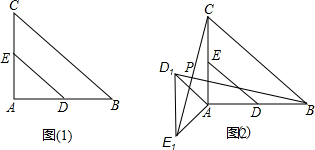如图（1），在Rt△ABC中，∠A=90°，AC=AB=4，D，E分别是AB，AC的中点．若等腰Rt△ADE绕点A逆时针旋转，得到等腰Rt△AD1E1，如图（2），设旋转角为α（0＜α≤180°），记直线BD1与CE1的交点为P．
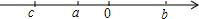已知实数a，b，c关系是a＜0，b＞0，c＜0，且|c|＞|b|＞|a|．