题目内容
12.已知多项式x3+ax2+bx+c含有因式x+1和x-1,且被x-2除余数为3,那么a=-1;b=-1;c=1.分析 由多项式x3+ax2+bx+c含有因式x+1和x-1可得x3+ax2+bx+c=(x+1)(x-1)(mx+n),分别令x=±1,可得关于a、b、c的俩方程;再由多项式x3+ax2+bx+c被x-2除余数为3可得x3+ax2+bx+c=p(x-2)+3,令x=2可得关于a、b、c的方程,联立方程组求解可得.
解答 解:∵多项式x3+ax2+bx+c含有因式x+1和x-1,
∴x3+ax2+bx+c=(x+1)(x-1)(mx+n),
当x=1时,1+a+b+c=0,即a+b+c=-1,
当x=-1时,-1+a-b+c=0,即a-b+c=1,
又∵多项式x3+ax2+bx+c被x-2除余数为3,
∴x3+ax2+bx+c=p(x-2)+3,
当x=2时,8+4a+2b+c=3,即4a+2b+c=-5,
联立可得方程组$\left\{\begin{array}{l}{a+b+c=-1}\\{a-b+c=1}\\{4a+2b+c=-5}\end{array}\right.$,
解得:a=-1,b=-1,c=1,
故答案为:-1,-1,1.
点评 本题主要考查因式定理与综合除法的知识点,解答本题的关键是熟练掌握整除带余的概念.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 OB.
OB.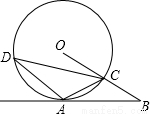
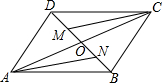 如图.在?ABCD中.对角线AC,BD交于点O,M,N分别是OD,OB的中点,连接CM,AN.
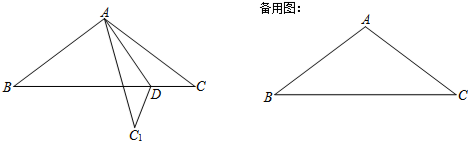
如图.在?ABCD中.对角线AC,BD交于点O,M,N分别是OD,OB的中点,连接CM,AN.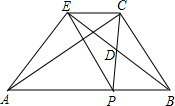 如图,在Rt△ABC中,∠ACB=90°,点P是斜边AB上一个动点(不与A、B重合),连接PC,点D是PC的中点,连接BD并延长至E,使DE=BD,连接EA、EP、EC.
如图,在Rt△ABC中,∠ACB=90°,点P是斜边AB上一个动点(不与A、B重合),连接PC,点D是PC的中点,连接BD并延长至E,使DE=BD,连接EA、EP、EC.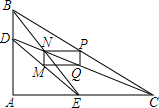 已知:在△ABC中,∠A=90°,D,E分别是AB,AC上任意一点,M,N,P,Q分别是DE,BE,BC,CD的中点,求证:四边形PQMN是矩形.
已知:在△ABC中,∠A=90°,D,E分别是AB,AC上任意一点,M,N,P,Q分别是DE,BE,BC,CD的中点,求证:四边形PQMN是矩形.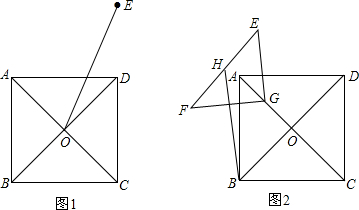
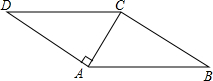 如图,在?ABCD中,AC⊥AD,∠B=30°,AC=2,则?ABCD的周长是4$\sqrt{3}$+8.
如图,在?ABCD中,AC⊥AD,∠B=30°,AC=2,则?ABCD的周长是4$\sqrt{3}$+8. 如图为实数a,b在数轴上的位置,则($\sqrt{b}$)2+$\sqrt{(-a)^{2}}$-$\sqrt{(a-b)^{2}}$=0.
如图为实数a,b在数轴上的位置,则($\sqrt{b}$)2+$\sqrt{(-a)^{2}}$-$\sqrt{(a-b)^{2}}$=0.