题目内容
18.已知抛物线的顶点坐标是A(1,4)且经过点B(0,3)①求抛物线的解析式;
②求抛物线与x轴交点的坐标C和D(C在D的左侧);
③求三角形BCA的面积.
分析 ①利用待定系数法即可求得抛物线的解析式;
②令y=0,即可得到关于x的方程求得C和D的横坐标;
③求得C的坐标,然后利用三角形的面积公式求解.
解答 解:①设抛物线的解析式是y=a(x-1)2+4,
则a+4=3,
解得:a=-1.
则抛物线的解析式是y=-(x-1)2+4,即y=-x2+2x+3;
②在y=-x2+2x+3中令y=0,则-x2+2x+3=0,解得:x=-1或3,
则C的坐标是(-1,0),D的坐标是(3,0);
③在y=-x2+2x+3中令x=0,则y=3,
CD=3-(-1)=4,则△BCA的面积是$\frac{1}{2}$×4×3=6.
点评 本题考查了待定系数法求函数的解析式以及函数与x轴、y轴的交点坐标的求法,是一个基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 B.
B.  C.
C.  D.
D. 
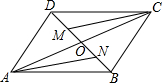 如图.在?ABCD中.对角线AC,BD交于点O,M,N分别是OD,OB的中点,连接CM,AN.
如图.在?ABCD中.对角线AC,BD交于点O,M,N分别是OD,OB的中点,连接CM,AN.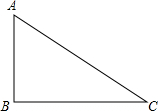 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.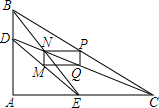 已知:在△ABC中,∠A=90°,D,E分别是AB,AC上任意一点,M,N,P,Q分别是DE,BE,BC,CD的中点,求证:四边形PQMN是矩形.
已知:在△ABC中,∠A=90°,D,E分别是AB,AC上任意一点,M,N,P,Q分别是DE,BE,BC,CD的中点,求证:四边形PQMN是矩形.