题目内容
8．
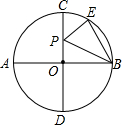如图，AB、CD是⊙O的两条直径，且AB⊥CD，$\widehat{CE}$=$\frac{1}{2}$$\widehat{EB}$，P为直径CD上一动点，若⊙O的直径AB=2，则△PEB周长的最小值是（ ）| A． | 3 | B． | 4 | C． | 2$\sqrt{3}$ | D． | $\sqrt{3}$+1 |
分析 连接AE交CD于P，则△PEB周长的最小值=AE+BE，根据已知条件得到∠A=30°，解直角三角形得到BE=1，AE=$\sqrt{3}$，于是得到结论．
解答 
解：连接AE交CD于P，
则△PEB周长的最小值=AE+BE，
∵AB、CD是⊙O的两条直径，且AB⊥CD，$\widehat{CE}$=$\frac{1}{2}$$\widehat{EB}$，
∴∠A=30°，
∵AB是⊙O的直径，
∴∠AEB=90°，
∵AB=2，
∴BE=1，AE=$\sqrt{3}$，
∴△PEB周长的最小值=$\sqrt{3}$+1，
故选D．
点评 本题考查了轴对称-最短距离问题，圆周角定理，解直角三角形，正确的周长图形是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知，如图，在同一坐标系中，直线AB：y=-0.5x+1与y轴交于点B，直线AC：y=2x-1与y轴交于点C，两条直线AB与AC的交点为A．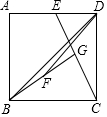
如图，在正方形ABCD中，E为AD的中点，G为CE的中点，F为BG的中点，连结DF，DB，若S△BGC=2，则边长BC=2$\sqrt{2}$，S△BFD=$\frac{1}{2}$．
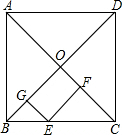如图，在正方形ABCD中，E为BC上任意一点，EF⊥AC于F，EG⊥BD于F，试说明：EF+EG=OB．
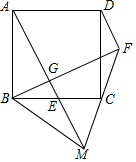如图，正方形ABCD中，E为BC上一点，过B作BG⊥AE于G，延长BG⊥AE于G，延长BG至点F使∠CFB=45°，延长FC、AE交于点M，连接DF、BM，若C为FM中点，BM=10，则FD的长为2$\sqrt{5}$．