题目内容
2. 已知,如图,在同一坐标系中,直线AB:y=-0.5x+1与y轴交于点B,直线AC:y=2x-1与y轴交于点C,两条直线AB与AC的交点为A.
已知,如图,在同一坐标系中,直线AB:y=-0.5x+1与y轴交于点B,直线AC:y=2x-1与y轴交于点C,两条直线AB与AC的交点为A.(1)求A的坐标;
(2)求证:直线AB⊥AC;
(3)请直接写出k1,k2满足的关系式.使得直线y=k1x+b1(k1≠0)和直线y=k2x+b2(k2≠0)相垂直.
分析 (1)两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解.
(2)根据各点的坐标,得到BC=2,AB=$\frac{2}{5}\sqrt{5}$,AC=$\frac{4}{5}\sqrt{5}$,据此可得AB2+AC2=BC2,进而得到AB⊥AC;
(3)根据坐标平面内两条互相垂直的直线的系数k的乘积为-1进行判断.
解答 解:(1)解方程组$\left\{\begin{array}{l}{y=-0.5x+1}\\{y=2x-1}\end{array}\right.$,
可得$\left\{\begin{array}{l}{x=\frac{4}{5}}\\{y=\frac{3}{5}}\end{array}\right.$,
∴A的坐标为($\frac{4}{5}$,$\frac{3}{5}$);
(2)∵直线AB:y=-0.5x+1与y轴交于点B(0,1),直线AC:y=2x-1与y轴交于点C(0,-1),
∴BC=2,AB=$\sqrt{(\frac{4}{5})^{2}+(\frac{3}{5}-1)^{2}}$=$\frac{2}{5}\sqrt{5}$,AC=$\sqrt{(\frac{4}{5})^{2}+(\frac{3}{5}+1)^{2}}$=$\frac{4}{5}\sqrt{5}$,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,且∠BAC=90°,
∴AB⊥AC;
(3)若直线y=k1x+b1(k1≠0)和直线y=k2x+b2(k2≠0)相垂直,则k1×k2=-1.
点评 本题主要考查了两条直线的交点问题,解题时注意:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解.

练习册系列答案
相关题目
12.某校组织学生到距学校6km的光明科技馆参观,准备乘出租车去科技馆,出租车的收费标准如表:
则收费y(元)与出租车行驶里程数x(km)(x≥3)之间的关系式为( )
| 里程数 | 收费/元 |
| 3km以下(含3km) | 8.00 |
| 3km以上每增加1km | 1.80 |
| A. | y=8x | B. | y=1.8x | C. | y=8+1.8x | D. | y=2.6+1.8x |
13. 有理数a,b在数轴上的位置如图所示,则下面关系式中正确的个数是( )
有理数a,b在数轴上的位置如图所示,则下面关系式中正确的个数是( )
①a-b<0;②a+b>0;③$\frac{1}{a}>\frac{1}{b}$;④ab>0.
 有理数a,b在数轴上的位置如图所示,则下面关系式中正确的个数是( )
有理数a,b在数轴上的位置如图所示,则下面关系式中正确的个数是( )①a-b<0;②a+b>0;③$\frac{1}{a}>\frac{1}{b}$;④ab>0.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.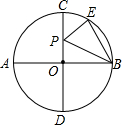 如图,AB、CD是⊙O的两条直径,且AB⊥CD,$\widehat{CE}$=$\frac{1}{2}$$\widehat{EB}$,P为直径CD上一动点,若⊙O的直径AB=2,则△PEB周长的最小值是( )
如图,AB、CD是⊙O的两条直径,且AB⊥CD,$\widehat{CE}$=$\frac{1}{2}$$\widehat{EB}$,P为直径CD上一动点,若⊙O的直径AB=2,则△PEB周长的最小值是( )
 如图,AB、CD是⊙O的两条直径,且AB⊥CD,$\widehat{CE}$=$\frac{1}{2}$$\widehat{EB}$,P为直径CD上一动点,若⊙O的直径AB=2,则△PEB周长的最小值是( )
如图,AB、CD是⊙O的两条直径,且AB⊥CD,$\widehat{CE}$=$\frac{1}{2}$$\widehat{EB}$,P为直径CD上一动点,若⊙O的直径AB=2,则△PEB周长的最小值是( )| A. | 3 | B. | 4 | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$+1 |
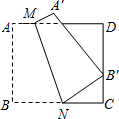 如图,四边形ABCD是边长为8的正方形纸片,将其沿MN折叠,使点B落在CD边上的B′处,点A的对应点为A′,且B′C=4.
如图,四边形ABCD是边长为8的正方形纸片,将其沿MN折叠,使点B落在CD边上的B′处,点A的对应点为A′,且B′C=4. 如图,长方形ABCD的边AB比BC大2,且恰好被分成6个正方形,则这个长方形的周长是48.
如图,长方形ABCD的边AB比BC大2,且恰好被分成6个正方形,则这个长方形的周长是48.