题目内容
19．若tanA=3，则$\frac{sinA•cosA-si{n}^{2}A}{1+3sinA•cosA}$=-$\frac{6}{19}$．分析 首先得出sinA=3cosA，进而代入原式求出答案．
解答 解：∵tanA=$\frac{sinA}{cosA}$=3，
∴sinA=3cosA，
∴原式=$\frac{3cosA•cosA-（3cosA）^{2}}{（3cosA）^{2}+co{s}^{2}A+3（3cosA）•cosA}$
=$\frac{-6co{s}^{2}A}{19co{s}^{2}A}$
=-$\frac{6}{19}$．
故答案为：-$\frac{6}{19}$．
点评 此题主要考查了同角三角函数的关系，正确得出sinA=3cosA是解题关键．
练习册系列答案
相关题目
13．
有理数a，b在数轴上的位置如图所示，则下面关系式中正确的个数是（ ）
①a-b＜0；②a+b＞0；③$\frac{1}{a}＞\frac{1}{b}$；④ab＞0．
有理数a，b在数轴上的位置如图所示，则下面关系式中正确的个数是（ ）①a-b＜0；②a+b＞0；③$\frac{1}{a}＞\frac{1}{b}$；④ab＞0．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
14．
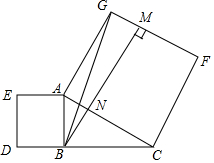如图，在Rt△ABC中，∠ABC=90°，分别以AB、AC为边向外作正方形ABDE和正方形ACFG，过点B作BM⊥GF，垂足为M，BM交AC于点N，连接BG，CE，下列结论中，不正确的是（ ）
如图，在Rt△ABC中，∠ABC=90°，分别以AB、AC为边向外作正方形ABDE和正方形ACFG，过点B作BM⊥GF，垂足为M，BM交AC于点N，连接BG，CE，下列结论中，不正确的是（ ）| A． | BG=CE | B． | BG⊥CE | ||
| C． | S正方形ABDE＞S四边形ANMG | D． | BC2=CF•FM |
4．
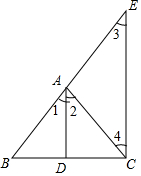如图，∠1=∠2，EC∥AD．
求证：∠3=∠4．
证明：∵EC∥AD，
∴∠1=∠3（两直线平行，同位角相等），
∠2=∠4（两直线平行，内错角相等），
又∵∠1=∠2（已知），
∴∠3=∠4（等量代换）．
如图，∠1=∠2，EC∥AD．求证：∠3=∠4．
证明：∵EC∥AD，
∴∠1=∠3（两直线平行，同位角相等），
∠2=∠4（两直线平行，内错角相等），
又∵∠1=∠2（已知），
∴∠3=∠4（等量代换）．
8．
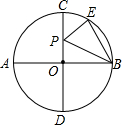如图，AB、CD是⊙O的两条直径，且AB⊥CD，$\widehat{CE}$=$\frac{1}{2}$$\widehat{EB}$，P为直径CD上一动点，若⊙O的直径AB=2，则△PEB周长的最小值是（ ）
如图，AB、CD是⊙O的两条直径，且AB⊥CD，$\widehat{CE}$=$\frac{1}{2}$$\widehat{EB}$，P为直径CD上一动点，若⊙O的直径AB=2，则△PEB周长的最小值是（ ）| A． | 3 | B． | 4 | C． | 2$\sqrt{3}$ | D． | $\sqrt{3}$+1 |
9．
如图，点D、E、F分别是AB、BC、CA的中点，则图中平行四边形一共有（ ）
如图，点D、E、F分别是AB、BC、CA的中点，则图中平行四边形一共有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |