题目内容
13.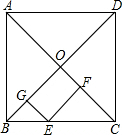 如图,在正方形ABCD中,E为BC上任意一点,EF⊥AC于F,EG⊥BD于F,试说明:EF+EG=OB.
如图,在正方形ABCD中,E为BC上任意一点,EF⊥AC于F,EG⊥BD于F,试说明:EF+EG=OB.
分析 根据条件可以得到四边形GEOF是矩形,因而EF=OG,同时易证△BEG是等腰直角三角形,因而EG=BG,则EF+EG=OB.
解答 证明:∵四边形ABCD是正方形,
∴AC⊥BD,∠CBO=45°
∵EF⊥AC,GE⊥BD,
∴∠OGE=∠OFE=90°;
又∵AC⊥BD,
∴四边形OGEF是矩形;
∴EF=OG,
又∵∠EBG=∠BEG=45°,
∴EG=BG,
∴EF+EG=OB.
点评 本题考查了正方形的对角线互相垂直平分的性质,对角线平分一组对角的性质,等腰直角三角形的性质,以及矩形的判定与性质,熟记性质是解题的关键.

练习册系列答案
相关题目
4.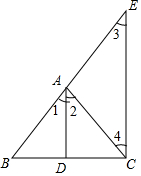 如图,∠1=∠2,EC∥AD.
如图,∠1=∠2,EC∥AD.
求证:∠3=∠4.
证明:∵EC∥AD,
∴∠1=∠3(两直线平行,同位角相等),
∠2=∠4(两直线平行,内错角相等),
又∵∠1=∠2(已知),
∴∠3=∠4(等量代换).
 如图,∠1=∠2,EC∥AD.
如图,∠1=∠2,EC∥AD.求证:∠3=∠4.
证明:∵EC∥AD,
∴∠1=∠3(两直线平行,同位角相等),
∠2=∠4(两直线平行,内错角相等),
又∵∠1=∠2(已知),
∴∠3=∠4(等量代换).
8.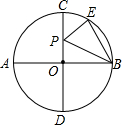 如图,AB、CD是⊙O的两条直径,且AB⊥CD,$\widehat{CE}$=$\frac{1}{2}$$\widehat{EB}$,P为直径CD上一动点,若⊙O的直径AB=2,则△PEB周长的最小值是( )
如图,AB、CD是⊙O的两条直径,且AB⊥CD,$\widehat{CE}$=$\frac{1}{2}$$\widehat{EB}$,P为直径CD上一动点,若⊙O的直径AB=2,则△PEB周长的最小值是( )
 如图,AB、CD是⊙O的两条直径,且AB⊥CD,$\widehat{CE}$=$\frac{1}{2}$$\widehat{EB}$,P为直径CD上一动点,若⊙O的直径AB=2,则△PEB周长的最小值是( )
如图,AB、CD是⊙O的两条直径,且AB⊥CD,$\widehat{CE}$=$\frac{1}{2}$$\widehat{EB}$,P为直径CD上一动点,若⊙O的直径AB=2,则△PEB周长的最小值是( )| A. | 3 | B. | 4 | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$+1 |
5.下列说法正确的是( )
| A. | 四边形的对角线互相平分 | |
| B. | 一组对边平行,另一组对边相等的四边形是平行四边形 | |
| C. | 线段的垂直平分线上的点到线段两个端点的距离相等 | |
| D. | 两边对应成比例且有一个角对应相等的两个三角形相似 |
2.一次函数y=-(m2+1)x-(m2+2)的图象(m为常数)不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.下列函数经过一、二、四象限的是( )
| A. | y=2x+1 | B. | y=-2x+1 | C. | y=2x-1 | D. | y=-2x-1 |
 如图,长方形ABCD的边AB比BC大2,且恰好被分成6个正方形,则这个长方形的周长是48.
如图,长方形ABCD的边AB比BC大2,且恰好被分成6个正方形,则这个长方形的周长是48.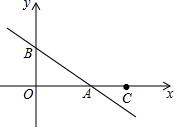 如图,直线y=-$\frac{2}{3}$x+m分别交x轴、y轴于A、B两点,已知点C(6,0).
如图,直线y=-$\frac{2}{3}$x+m分别交x轴、y轴于A、B两点,已知点C(6,0).