题目内容
16.半径相等的正三角形与正四边形的边心距之比为1:$\sqrt{2}$.分析 根据题意可以求得半径为r的圆内接正三角形,正四边形的边心距,从而可以求得它们的比值.
解答 解:设半径=r,由题意可得,
正三角形的边心距是:r•sin30°=$\frac{1}{2}$r,
正四边形的边心距是:r×sin45°=$\frac{\sqrt{2}}{2}$r,
半径相等的正三角形,正四边形的边心距之比为:1:$\sqrt{2}$,
故答案为:1:$\sqrt{2}$.
点评 本题考查正多边形和圆,解答本题的关键是明确题意,求出相应的图形的边心距.

练习册系列答案
相关题目
4.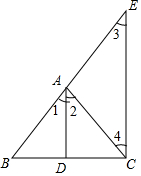 如图,∠1=∠2,EC∥AD.
如图,∠1=∠2,EC∥AD.
求证:∠3=∠4.
证明:∵EC∥AD,
∴∠1=∠3(两直线平行,同位角相等),
∠2=∠4(两直线平行,内错角相等),
又∵∠1=∠2(已知),
∴∠3=∠4(等量代换).
 如图,∠1=∠2,EC∥AD.
如图,∠1=∠2,EC∥AD.求证:∠3=∠4.
证明:∵EC∥AD,
∴∠1=∠3(两直线平行,同位角相等),
∠2=∠4(两直线平行,内错角相等),
又∵∠1=∠2(已知),
∴∠3=∠4(等量代换).
8.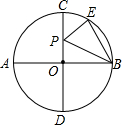 如图,AB、CD是⊙O的两条直径,且AB⊥CD,$\widehat{CE}$=$\frac{1}{2}$$\widehat{EB}$,P为直径CD上一动点,若⊙O的直径AB=2,则△PEB周长的最小值是( )
如图,AB、CD是⊙O的两条直径,且AB⊥CD,$\widehat{CE}$=$\frac{1}{2}$$\widehat{EB}$,P为直径CD上一动点,若⊙O的直径AB=2,则△PEB周长的最小值是( )
 如图,AB、CD是⊙O的两条直径,且AB⊥CD,$\widehat{CE}$=$\frac{1}{2}$$\widehat{EB}$,P为直径CD上一动点,若⊙O的直径AB=2,则△PEB周长的最小值是( )
如图,AB、CD是⊙O的两条直径,且AB⊥CD,$\widehat{CE}$=$\frac{1}{2}$$\widehat{EB}$,P为直径CD上一动点,若⊙O的直径AB=2,则△PEB周长的最小值是( )| A. | 3 | B. | 4 | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$+1 |
5.下列说法正确的是( )
| A. | 四边形的对角线互相平分 | |
| B. | 一组对边平行,另一组对边相等的四边形是平行四边形 | |
| C. | 线段的垂直平分线上的点到线段两个端点的距离相等 | |
| D. | 两边对应成比例且有一个角对应相等的两个三角形相似 |
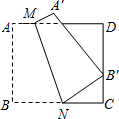 如图,四边形ABCD是边长为8的正方形纸片,将其沿MN折叠,使点B落在CD边上的B′处,点A的对应点为A′,且B′C=4.
如图,四边形ABCD是边长为8的正方形纸片,将其沿MN折叠,使点B落在CD边上的B′处,点A的对应点为A′,且B′C=4. 某互联网公司对用户实行两种收费方式:
某互联网公司对用户实行两种收费方式: