题目内容
15.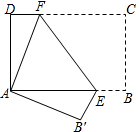 如图,将矩形纸片ABCD折叠,使点C与点A重合(折痕为EF),剪去不折叠的部分.
如图,将矩形纸片ABCD折叠,使点C与点A重合(折痕为EF),剪去不折叠的部分.(1)观察:图中不重叠的两部分(即△ADF与△AB′E′)是否全等?请说明理由;
(2)思考:将重叠部分展开,得到的四边形是什么四边形?并证明你的结论.
分析 (1)利用两角夹边对应相等的两个三角形全等即可判定.
(2)先证明四边形AECF是平行四边形,再证明邻边相等是菱形即可.
解答 解:(1)结论:△ADF≌△AB′E.
理由:∵四边形ABCD是矩形,
∴∠D=∠C=∠B′=90°,AD=CB=AB′,
∵∠DAF+∠EAF=90°,∠B′AE+∠EAF=90°,
∴∠DAF=∠B′AE,
在△ADF和△AB′E中,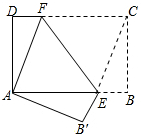
$\left\{\begin{array}{l}{∠D=∠B′}\\{AD=AB′}\\{∠DAF=∠EAB′}\end{array}\right.$,
∴△ADF≌△AB′E.
(2)结论:四边形AECF是菱形.
理由:连接CE,由折叠可知,AF=CF,
∵△ADF≌△AB′E,
∴AF=AE,AE=CF,
∵AE∥CF,
∴四边形AECF是平行四边形,
∵AF=AE,
∴四边形AECF是菱形.
点评 本题考查翻折变换、全等三角形的判定和性质、熟练利用翻折不变性是解决问题的关键,记住菱形的三种判定方法,属于中考常考题型.

练习册系列答案
相关题目
4.下列四个数中,是无理数的是( )
| A. | $\frac{π}{2}$ | B. | $\frac{22}{7}$ | C. | $\root{3}{-8}$ | D. | ($\sqrt{3}$)2 |
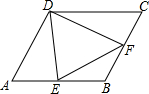 在菱形ABCD中,∠A=60°,E、F分别在AB,BC上,若△DEF有一个角为60°,求证:△DEF一定是等边三角形.
在菱形ABCD中,∠A=60°,E、F分别在AB,BC上,若△DEF有一个角为60°,求证:△DEF一定是等边三角形. 如图,在平面直角坐标系中,⊙D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.
如图,在平面直角坐标系中,⊙D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.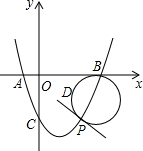 如图,抛物线y=x2-2x-3与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,点D的坐标为(1,-1),P是第四象限内抛物线上一动点,以PB为直径的圆经过点D,求经过点P且和这个圆相切的直线的解析式.
如图,抛物线y=x2-2x-3与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,点D的坐标为(1,-1),P是第四象限内抛物线上一动点,以PB为直径的圆经过点D,求经过点P且和这个圆相切的直线的解析式.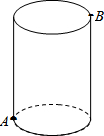 如图,圆柱的高为8cm,底面半径为2cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,它需要爬行的最短路程是多少厘米?(圆周率取3)
如图,圆柱的高为8cm,底面半径为2cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,它需要爬行的最短路程是多少厘米?(圆周率取3)