题目内容
9.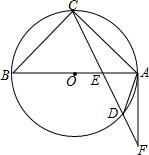 如图,已知AB是⊙O的直径,弦CD与AB交于点E,过点A作⊙O的切线与CD长线交于点F,AC=8,CE:ED=6:5,AE:EB=2:3.求:
如图,已知AB是⊙O的直径,弦CD与AB交于点E,过点A作⊙O的切线与CD长线交于点F,AC=8,CE:ED=6:5,AE:EB=2:3.求:(1)AB的长度;
(2)tan∠ECB的值.
分析 (1)设CE=6k,ED=5k,AE=2a,BE=3a,过点O作OH⊥CD垂足为H,则CH=HD,由△OHE∽△FAE,得$\frac{HE}{OE}$=$\frac{AE}{EF}$求出EF=$\frac{2{a}^{2}}{k}$,由CE•ED=BE•AE求出k、a关系,得EF=10k,得到DE=DC,得△DEA、△BCE都是等腰三角形,在RT△ABC中利用勾股定理即可解决问题.
(2)根据tan∠ECB=tan∠AEF=$\frac{AF}{AE}$,求出AF、AE即可.
解答 解:(1)设CE=6k,ED=5k,AE=2a,BE=3a,
过点O作OH⊥CD垂足为H,则CH=HD,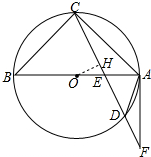 ∴EH=0.5k,OE=0.5a,
∴EH=0.5k,OE=0.5a,
∵AF是切线,
∴∠FAE=90°=∠OHE,
∵∠OEH=∠FEA,
∴△OHE∽△FAE,
∴$\frac{HE}{OE}$=$\frac{AE}{EF}$即$\frac{0.5k}{0.5a}$=$\frac{2a}{EF}$,
∴EF=$\frac{2{a}^{2}}{k}$,
∵CE•ED=BE•AE,
∴6k•5k=3a•2a,
∴a2=5k2,
∴EF=10k,
∴点D是EF中点,
∴AD=ED=DF=5k,
∴△DEA、△BCE都是等腰三角形,
∴BC=BE=3a,
∵AB是直径,
∴∠ACB=90°,
∴BC2+AC2=AB2,
∴(3a)2+82=(5a)2,
∴a=2,
∴AB=5a=10.
(2)∵a=2,
∴k=$\frac{2\sqrt{5}}{5}$,
∵AF2=DF•FC=80k2=64,
∴AF=8,
∴tan∠ECB=tan∠AEF=$\frac{AF}{AE}$=$\frac{8}{4}$=2.
点评 本题考查切线的性质、垂径定理、直角三角形斜边中线性质、等腰三角形的性质、勾股定理等知识,解题的关键是设两个参数,想办法求出EF的长,发现点D是EF中点这个突破口,题目比较难,属于中考压轴题.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案| A. | x2=-2 | B. | (x+2)2=x(x-1) | C. | $\frac{1}{{x}^{2}}$$+\frac{2}{x}$=1 | D. | x2-2x+y=0 |
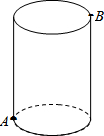 如图,圆柱的高为8cm,底面半径为2cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,它需要爬行的最短路程是多少厘米?(圆周率取3)
如图,圆柱的高为8cm,底面半径为2cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,它需要爬行的最短路程是多少厘米?(圆周率取3)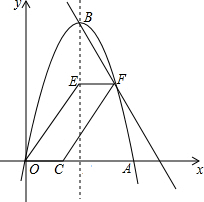 如图,抛物线y=-x2+6x与x轴交于点O,A,顶点为B,动点E在抛物线对称轴上,点F在对称轴右侧抛物线上,点C在x轴正半轴上,且EF$\stackrel{∥}{=}$OC,连接OE,CF得四边形OCFE.
如图,抛物线y=-x2+6x与x轴交于点O,A,顶点为B,动点E在抛物线对称轴上,点F在对称轴右侧抛物线上,点C在x轴正半轴上,且EF$\stackrel{∥}{=}$OC,连接OE,CF得四边形OCFE.