题目内容
10.在?ABCD中,E是BC的中点,F是BE的中点,AE与DF相交于H,则△EFH的面积与△ADH的面积的比值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{16}$ | D. | $\frac{1}{4}$ |
分析 根据已知可得到△EFH∽△ADH,及EF与AD的关系,从而根据相似三角形的面积比等于相似比的平方得到答案.
解答 解:由已知得,EF= $\frac{1}{4}$BC=$\frac{1}{4}$AD.
$\frac{1}{4}$BC=$\frac{1}{4}$AD.
∵AD∥BC,
∴△EFH∽△ADH,
∴相似比是1:4,
∴S△EFH:S△ADH=1:16.
故选C.
点评 本题考查平行四边形的性质、相似三角形的性质,解题的关键是熟练掌握相似三角形的面积的比等于相似比的平方.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
15.下列函数中,经过一、二、四象限的函数是( )
| A. | y=7 | B. | y=-2x | C. | y=-2x-7 | D. | y=-2x+7 |
18. 如图,AB∥CD,若∠1=40°,∠2=65°,则∠CAD=( )
如图,AB∥CD,若∠1=40°,∠2=65°,则∠CAD=( )
 如图,AB∥CD,若∠1=40°,∠2=65°,则∠CAD=( )
如图,AB∥CD,若∠1=40°,∠2=65°,则∠CAD=( )| A. | 50° | B. | 65° | C. | 75° | D. | 85° |
2.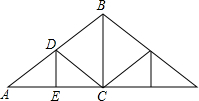 如图,屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=8m,∠A=30°,则BC和DE的长分别等于( )
如图,屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=8m,∠A=30°,则BC和DE的长分别等于( )
 如图,屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=8m,∠A=30°,则BC和DE的长分别等于( )
如图,屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=8m,∠A=30°,则BC和DE的长分别等于( )| A. | 2m,2m | B. | 4m,2m | C. | 2m,4m | D. | 4m,4m |
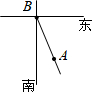 如图,如果张江高科技园区(A)位于复旦大学(B)的南偏东30°的方向,那么复旦大学(B)位于张江高科技园区(A)的北偏西30°或西偏北60°方向.
如图,如果张江高科技园区(A)位于复旦大学(B)的南偏东30°的方向,那么复旦大学(B)位于张江高科技园区(A)的北偏西30°或西偏北60°方向.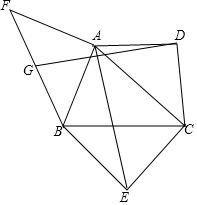 如图所示,已知△ABC是锐角三角形,以边AC、BC为斜边向形外作等腰直角三角形ACD和等腰直角三角形BCE,以边AB为直角边向形外作等腰直角三角形ABF,∠BAF=90°,点G为BF的中点,连接GD和AE,试探究GD和AE的数量关系和位置关系,并对你的结论加以证明.
如图所示,已知△ABC是锐角三角形,以边AC、BC为斜边向形外作等腰直角三角形ACD和等腰直角三角形BCE,以边AB为直角边向形外作等腰直角三角形ABF,∠BAF=90°,点G为BF的中点,连接GD和AE,试探究GD和AE的数量关系和位置关系,并对你的结论加以证明.