题目内容
5.小明准备用一段长30米的篱笆围成一个三角形形状的小圈,用于饲养家兔.已知第一条边长为a米,由于受地势限制,第二条边长只能是第一条边长的2倍多2米.(1)请用a表示第三条边长.
(2)问第一条边长可以为7米吗?为什么?请说明理由.
(3)求出a的取值范围.
(4)能否使得围成的小圈是直角三角形形状,且各边长均为整数?若能,说出你的围法;若不能,请说明理由.
分析 (1)本题需先表示出第二条边长,即可得出第三条边长;
(2)本题需先根据a=7,求出三边的长,根据三角形三边关系进行判断;
(3)根据三角形的三边关系列出不等式组,即可求出a的取值范围;
(3)本题需先求出a的值,然后即可得出三角形的三边长.
解答 解:(1)∵第二条边长为(2a+2)米,
∴第三条边长为30-a-(2a+2)=28-3a(米);
(2)不能.
当a=7时,三边长分别为7,16,7,
由于7+7<16,所以不能构成三角形,
即第一条边长不能为7m;
(3)根据题意得:
$\left\{\begin{array}{l}{a+2a+2>28-3a}\\{a+28-3a>2a+2}\\{2a+2+28-3a>a}\end{array}\right.$,
解得:$\frac{13}{3}$<a<$\frac{13}{2}$,
即a的取值范围是$\frac{13}{3}$<a<$\frac{13}{2}$.
(4)能围成.
在(3)的条件下,a为整数时,a只能取5或6.
当a=5时,三角形的三边长分别为5,12,13.
由52+122=132知,恰好能构成直角三角形.
当a=6时,三角形的三边长分别为6,14,10.
由62+102≠142知,此时不能构成直角三角形.
综上所述,能围成满足条件的小圈,它们的三边长分别为5m,12m,13m.
点评 本题主要考查了勾股定理、三角形三边关系以及一元一次不等式组的应用,在解题时根据三角形的三边关系,列出不等式组是本题的关键.

练习册系列答案
相关题目
11.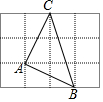 如图,将△ABC放在正方形网格中(图中每个小正方形边长均为1)点A,B,C恰好在网格图中的格点上,那么∠ABC的度数为( )
如图,将△ABC放在正方形网格中(图中每个小正方形边长均为1)点A,B,C恰好在网格图中的格点上,那么∠ABC的度数为( )
 如图,将△ABC放在正方形网格中(图中每个小正方形边长均为1)点A,B,C恰好在网格图中的格点上,那么∠ABC的度数为( )
如图,将△ABC放在正方形网格中(图中每个小正方形边长均为1)点A,B,C恰好在网格图中的格点上,那么∠ABC的度数为( )| A. | 90° | B. | 60° | C. | 30° | D. | 45° |
20.下列命题中,真命题是( )
| A. | 在同一平面内,过一点可作一条直线与已知直线垂直 | |
| B. | 过一点可作一条直线与已知直线平行 | |
| C. | 三条直线两两相交有三个交点 | |
| D. | 垂直于同一条直线的两条直线平行 |
10.在?ABCD中,E是BC的中点,F是BE的中点,AE与DF相交于H,则△EFH的面积与△ADH的面积的比值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{16}$ | D. | $\frac{1}{4}$ |
17.计算5-(-2)×3的结果等于( )
| A. | -11 | B. | -1 | C. | 1 | D. | 11 |
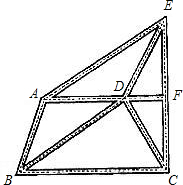 已知:如图是某城市部分街道示意图,AF∥BC,且AF⊥CE,AB=DC,AB∥DE,BD∥AE.甲、乙两人同时从B站乘车到F站,甲乘1路车,路线是B→A→E→F,乙乘2路车,路线是B→D→C→F,假设两车速度相同,途中耽误时间相同,那么谁先到达F站?说明理由.
已知:如图是某城市部分街道示意图,AF∥BC,且AF⊥CE,AB=DC,AB∥DE,BD∥AE.甲、乙两人同时从B站乘车到F站,甲乘1路车,路线是B→A→E→F,乙乘2路车,路线是B→D→C→F,假设两车速度相同,途中耽误时间相同,那么谁先到达F站?说明理由.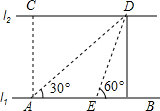 如图,河的两岸l1与l2互相平行,A、B是l1上的两点,C、D是l2上的两点,某同学在A处测得∠CAB=90°,∠DAB=30°,再沿AB方向走20米到达点E(即AE=20),测得∠DEB=60°.
如图,河的两岸l1与l2互相平行,A、B是l1上的两点,C、D是l2上的两点,某同学在A处测得∠CAB=90°,∠DAB=30°,再沿AB方向走20米到达点E(即AE=20),测得∠DEB=60°.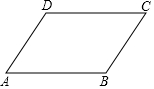 已知ABCD为平行四边形,求证:2(AB2+AD2)=AC2+BD2.
已知ABCD为平行四边形,求证:2(AB2+AD2)=AC2+BD2.