题目内容
18. 如图,AB∥CD,若∠1=40°,∠2=65°,则∠CAD=( )
如图,AB∥CD,若∠1=40°,∠2=65°,则∠CAD=( )| A. | 50° | B. | 65° | C. | 75° | D. | 85° |
分析 先根据平行线的性质,得到∠BAC的度数,再根据∠1=∠BAD=40°,即可得到∠CAD的度数.
解答 解:∵AB∥CD,∠2=65°,
∴∠BAC=180°-65°=115°,
又∵∠1=∠BAD=40°,
∴∠CAD=115°-40°=75°,
故选:C.
点评 本题主要考查了平行线的性质的运用,解题时注意:两直线平行,同旁内角互补.

练习册系列答案
相关题目
3.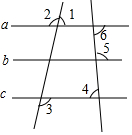 如图,下列命题是假命题的是( )
如图,下列命题是假命题的是( )
 如图,下列命题是假命题的是( )
如图,下列命题是假命题的是( )| A. | 如果∠2=∠3,那么a∥c | B. | 如果a∥b,a∥c,那么b∥c | ||
| C. | 如果∠4+∠5=180°,那么∠2=∠3 | D. | 如果∠4=∠6,那么∠1+∠3=180° |
10.在?ABCD中,E是BC的中点,F是BE的中点,AE与DF相交于H,则△EFH的面积与△ADH的面积的比值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{16}$ | D. | $\frac{1}{4}$ |
7.下列运算正确的是( )
| A. | a+a=a2 | B. | a2•a=a2 | C. | a3÷a2=a (a≠0) | D. | (a2)3=a5 |
8.某水果店有甲、乙两种苹果包装盒,现有360个苹果要用这两种包装盒进行包装,已知每个甲包装盒比每个乙
包装盒少装3个苹果,单独用甲包装盒比单独用乙包装盒多用6个,设每个甲包装盒可装x个苹果,根据题意
下面所列方程正确的是( )
包装盒少装3个苹果,单独用甲包装盒比单独用乙包装盒多用6个,设每个甲包装盒可装x个苹果,根据题意
下面所列方程正确的是( )
| A. | $\frac{360}{x}$=$\frac{360}{x-3}$+6 | B. | $\frac{360}{x}$=$\frac{360}{x+3}$+6 | C. | $\frac{360}{x-3}$=$\frac{360}{x}$+6 | D. | $\frac{360}{x+3}$=$\frac{360}{x}$+6 |
 如图,在△ABC中,AD是∠BAC平分线,AD的垂直平分线分别交AB,BC延长线于F,E,求证:
如图,在△ABC中,AD是∠BAC平分线,AD的垂直平分线分别交AB,BC延长线于F,E,求证: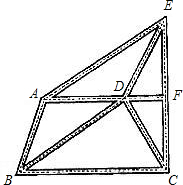 已知:如图是某城市部分街道示意图,AF∥BC,且AF⊥CE,AB=DC,AB∥DE,BD∥AE.甲、乙两人同时从B站乘车到F站,甲乘1路车,路线是B→A→E→F,乙乘2路车,路线是B→D→C→F,假设两车速度相同,途中耽误时间相同,那么谁先到达F站?说明理由.
已知:如图是某城市部分街道示意图,AF∥BC,且AF⊥CE,AB=DC,AB∥DE,BD∥AE.甲、乙两人同时从B站乘车到F站,甲乘1路车,路线是B→A→E→F,乙乘2路车,路线是B→D→C→F,假设两车速度相同,途中耽误时间相同,那么谁先到达F站?说明理由.