题目内容
17.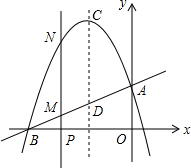 如图,已知直线y=$\frac{1}{2}$x+$\frac{7}{2}$与x轴、y轴分别相交于B、A两点,抛物线y=ax2+bx+c经过A、B两点,且对称轴为x=-3.
如图,已知直线y=$\frac{1}{2}$x+$\frac{7}{2}$与x轴、y轴分别相交于B、A两点,抛物线y=ax2+bx+c经过A、B两点,且对称轴为x=-3.(1)求A、B两点的坐标,并求抛物线的解析式;
(2)若点P以1个单位/秒的速度从点B沿x轴向点O运动,过点P作y轴的平行线交直线AB于点M,交抛物线于点N,设点P运动的时间为t,MN的长度为s,求s与t之间的函数关系式,并求出当t为何值时,s取得最大值?
分析 (1)根据直线的解析式分别令x=0、y=0,即可求得A、B的坐标,然后设出抛物线的顶点式,用待定系数法得到二次函数的解析式即可.
(2)设BP=t(0<t<7),则OP=7-t,P(t-7,0),M(t-7,$\frac{t}{2}$),N(t-7,-$\frac{1}{2}$(t-7+3)2+8),即可得出s=MN=-$\frac{1}{2}$t2+$\frac{7}{2}$t(0<t<7),由-$\frac{1}{2}$<0,可知S有最大值,然后根据二次函数的性质即可求得s的最大值.
解答 解:(1)∵直线y=$\frac{1}{2}$x+$\frac{7}{2}$与x轴、y轴分别相交于B、A两点,
∴令x=0,则y=$\frac{7}{2}$,令y=0,则x=-7,
∴A(0,$\frac{7}{2}$),B(-7,0),
∵抛物线的对称轴为直线x=-3.
∴设抛物线的解析式为y=a(x+3)2+n,
∵抛物线过A(0,$\frac{7}{2}$),B(-7,0),
∴$\left\{\begin{array}{l}{9a+n=\frac{7}{2}}\\{16a+n=0}\end{array}\right.$解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{n=8}\end{array}\right.$.
∴抛物线的解析式为y=-$\frac{1}{2}$(x+3)2+8.
(2)设BP=t(0<t<7),则OP=7-t,
∴P(t-7,0)
∵由于MP与y轴平行,且点M在直线AB上
∴M(t-7,$\frac{t}{2}$),
∵MN与y轴平行,且点N在抛物线上
∴N(t-7,-$\frac{1}{2}$(t-7+3)2+8),
∴s=MN=-$\frac{1}{2}$(t-7+3)2+8-$\frac{t}{2}$=-$\frac{1}{2}$t2+$\frac{7}{2}$t(0<t<7),
∵-$\frac{1}{2}$<0,即S有最大值
∴当t=-$\frac{\frac{7}{2}}{2×(-\frac{1}{2})}$=$\frac{7}{2}$时,s最大=-$\frac{1}{2}$×($\frac{7}{2}$)2+$\frac{7}{2}$×$\frac{7}{2}$=$\frac{49}{8}$.
点评 本题考查了待定系数法求二次函数的解析式和一次函数的解析式,在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.

 如图,将矩形ABCD沿DE折叠,点A恰好落在BC上的点F处,点G、H分别在AD、AB上,且FG⊥DH,若tan∠ADE=$\frac{1}{2}$,则$\frac{GF}{DH}$的值为( )
如图,将矩形ABCD沿DE折叠,点A恰好落在BC上的点F处,点G、H分别在AD、AB上,且FG⊥DH,若tan∠ADE=$\frac{1}{2}$,则$\frac{GF}{DH}$的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{5}$ |
| A. | $\frac{m}{m+1}$ | B. | $\frac{1}{m-1}$ | C. | $\frac{m}{m-1}$ | D. | m |
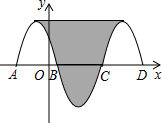 如图,抛物线y=-x2-2x+3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1关于点B的中心对称得C2,C2与x轴交于另一点C,将C2关于点C的中心对称得C3,连接C1与C3的顶点,则图中阴影部分的面积为32.
如图,抛物线y=-x2-2x+3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1关于点B的中心对称得C2,C2与x轴交于另一点C,将C2关于点C的中心对称得C3,连接C1与C3的顶点,则图中阴影部分的面积为32.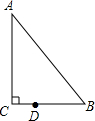 如图,在△ABC中,∠C=90°,∠B=55°,点D在BC边上,DB=2CD,若将△ABC绕点D逆时针旋转α度(0<α<180)后,点B恰好落在初始位置时△ABC的边上,则α等于70或120.
如图,在△ABC中,∠C=90°,∠B=55°,点D在BC边上,DB=2CD,若将△ABC绕点D逆时针旋转α度(0<α<180)后,点B恰好落在初始位置时△ABC的边上,则α等于70或120.