题目内容
7．
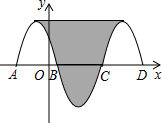如图，抛物线y=-x2-2x+3与x轴交于点A、B，把抛物线在x轴及其上方的部分记作C1，将C1关于点B的中心对称得C2，C2与x轴交于另一点C，将C2关于点C的中心对称得C3，连接C1与C3的顶点，则图中阴影部分的面积为32．
分析 将x轴下方的阴影部分沿对称轴分成两部分补到x轴上方，即可将不规则图形转换为规则的长方形，则可求出．
解答 解：∵抛物线y=-x2-2x+3与x轴交于点A、B，
∴当y=0时，则-x2-2x+3=0，
解得x=-3或x=1，
则A，B的坐标分别为（-3，0），（1，0），
AB的长度为4，
从C1，C3两个部分顶点分别向下作垂线交x轴于E、F两点．
根据中心对称的性质，x轴下方部分可以沿对称轴平均分成两部分补到C1与C2．
如图所示，阴影部分转化为矩形．
根据对称性，可得BE=CF=4÷2=2，则EF=8
利用配方法可得y=-x2-2x+3=-（x+1）2+4
则顶点坐标为（-1，4），即阴影部分的高为4，
S阴=8×4=32．
点评 本题考查了中心对称的性质、配方法求抛物线的顶点坐标及求抛物线与x轴交点坐标，解题关键是将不规则图形通过对称转换为规则图形，求阴影面积经常要使用转化的数学思想．
练习册系列答案
相关题目
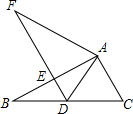如图，在△ABC中，∠BAC=90°，将△ABC绕点A顺时针旋转后，得到△ADF，此时点D落在边BC的中点处，则图中与∠C相等的角（除∠C外）有（ ）
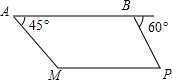如图，我巡逻机在海岛M上空巡逻，距离海平面垂直高度为1000米，在A点测得正前方海岛M的俯角为45°，在沿海面水平方向飞行2000米到达B点时测得一不明船只P的俯角为60°，已知A，B，P，M在同一水平面上，求不明船只P与海岛M之间的距离（结果保留根号）
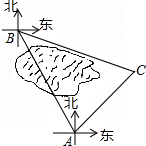五一期间，小明同学到滨湖湿地公园参加校无线电测向科技社团组织的实践活动，目标点B在观测点A北偏西30°方向，距观测点A直线距离600米．由于观测点A和目标点B之间被一片湿地分隔，无法直接通行，小明根据地形决定从观测点A出发，沿东北方向走一段距离后，到达位于目标点B南偏东75°方向的C处，求小明还要走多远才能到达目标点B？（结果保留根号）
如图，四边形ABCD是⊙O的内接四边形，∠ABC=2∠D，连接OA、OB、OC、AC，OB与AC相交于点E，若∠COB=3∠AOB，OC=2$\sqrt{3}$，则图中阴影部分面积是3π-2$\sqrt{3}$．（结果保留π和根号）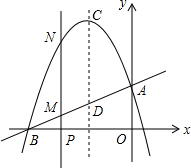
如图，已知直线y=$\frac{1}{2}$x+$\frac{7}{2}$与x轴、y轴分别相交于B、A两点，抛物线y=ax2+bx+c经过A、B两点，且对称轴为x=-3．