题目内容
5.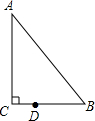 如图,在△ABC中,∠C=90°,∠B=55°,点D在BC边上,DB=2CD,若将△ABC绕点D逆时针旋转α度(0<α<180)后,点B恰好落在初始位置时△ABC的边上,则α等于70或120.
如图,在△ABC中,∠C=90°,∠B=55°,点D在BC边上,DB=2CD,若将△ABC绕点D逆时针旋转α度(0<α<180)后,点B恰好落在初始位置时△ABC的边上,则α等于70或120.
分析 根据题意画出符合的两种情况,①当B点落在AB上时,求出∠B=∠DB°,即可求出∠B′DB;②当B点落在AC上时,根据题意求出∠B′DC,即可求出∠B′DB的度数,即可得出答案.
解答 解:分为两种情况:①当B点落在AB上时,如图1,
∵根据旋转的性质得出DB=DB′,
∵∠B=55°,
∴∠DB′B=∠B=55°,
∴∠B′DB=180°-55°-55°=70°,
即此时α=70;
②当B点落在AC上时,如图2,
如图,∵△ABC绕着点D顺时针旋转α度后得到△A′B′C′,
∴B′D=BD,
∵BD=2CD,
∴B′D=2CD,
∵∠ACB=90°,
∴∠CB′D=30°,
∴∠B′DC=60°,
∴∠B′DB=180°-60°=120°,
即此时α=120;
故答案为:70或120.
点评 本题考查了旋转的性质,等腰三角形的性质,直角三角形的性质的应用,能求出∠B′DB的度数是解题的关键,作出图形更形象直观.

练习册系列答案
相关题目
20. 将一副直角三角板按如图方式放置,使直角顶点C重合,当DE∥BC时,∠α的度数是( )
将一副直角三角板按如图方式放置,使直角顶点C重合,当DE∥BC时,∠α的度数是( )
 将一副直角三角板按如图方式放置,使直角顶点C重合,当DE∥BC时,∠α的度数是( )
将一副直角三角板按如图方式放置,使直角顶点C重合,当DE∥BC时,∠α的度数是( )| A. | 105° | B. | 115° | C. | 95° | D. | 110° |
 如图,我巡逻机在海岛M上空巡逻,距离海平面垂直高度为1000米,在A点测得正前方海岛M的俯角为45°,在沿海面水平方向飞行2000米到达B点时测得一不明船只P的俯角为60°,已知A,B,P,M在同一水平面上,求不明船只P与海岛M之间的距离(结果保留根号)
如图,我巡逻机在海岛M上空巡逻,距离海平面垂直高度为1000米,在A点测得正前方海岛M的俯角为45°,在沿海面水平方向飞行2000米到达B点时测得一不明船只P的俯角为60°,已知A,B,P,M在同一水平面上,求不明船只P与海岛M之间的距离(结果保留根号) 如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2$\sqrt{3}$,则图中阴影部分面积是3π-2$\sqrt{3}$.(结果保留π和根号)
如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2$\sqrt{3}$,则图中阴影部分面积是3π-2$\sqrt{3}$.(结果保留π和根号)
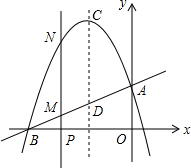 如图,已知直线y=$\frac{1}{2}$x+$\frac{7}{2}$与x轴、y轴分别相交于B、A两点,抛物线y=ax2+bx+c经过A、B两点,且对称轴为x=-3.
如图,已知直线y=$\frac{1}{2}$x+$\frac{7}{2}$与x轴、y轴分别相交于B、A两点,抛物线y=ax2+bx+c经过A、B两点,且对称轴为x=-3.