题目内容
19.在矩形ABCD中,AB=6,∠ABC的平分线交AD于点E,∠BED的平分线交矩形的边于点F,若点F恰为其所在矩形边的中点,则BC=3+3$\sqrt{2}$.(结果保留根号)分析 延长EF交BC于点G,首先证明△ABE为等腰直角三角形,并求得其斜边BE的长,然后根据条件判断三角形BEG为等腰三角形,最后根据△EFD≌△GFC得出CG与DE的相等关系,设CG=DE=x,并根据BG=BC+CG列出方程即可解决问题.
解答 解:延长EF和BC,交于点G,如图所示: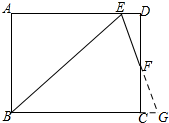
∵矩形ABCD中,∠B的角平分线BE与AD交于点E,
∴∠ABE=∠AEB=45°,
∴AB=AE=6,
∴等腰直角△ABE中,BE=$\sqrt{{6}^{2}+{6}^{2}}$=6 $\sqrt{2}$,
又∵∠BED的角平分线EF与DC交于点F,
∴∠BEG=∠DEF
∵AD∥BC
∴∠G=∠DEF
∴∠BEG=∠G
∴BG=BE=6 $\sqrt{2}$,
∵∠G=∠DEF,∠EFD=∠GFC,DF=FC
∴△EFD≌△GFC
∴CG=DE,
设CG=DE=x,则AD=6+x=BC,
∵BG=BC+CG,
∴6 $\sqrt{2}$=6+x+x,
解得:x=3 $\sqrt{2}$-3
∴BC=6+(3 $\sqrt{2}$-3)=3+3 $\sqrt{2}$;
故答案为:3+3 $\sqrt{2}$.
点评 本题主要考查了矩形、全等三角形的判定和性质、等腰三角形,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数构建方程解决问题.

练习册系列答案
相关题目
 如图,AO⊥BC,∠3=∠2,且∠3的补角比它的余角的2倍多30°,求∠1的度数.
如图,AO⊥BC,∠3=∠2,且∠3的补角比它的余角的2倍多30°,求∠1的度数. 如图所示,AB∥CD,AB,BE,ED,CD依次相交于B,E,D,猜想∠B,∠BED和∠D之间的数量关系,并说明理由.
如图所示,AB∥CD,AB,BE,ED,CD依次相交于B,E,D,猜想∠B,∠BED和∠D之间的数量关系,并说明理由.
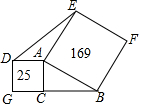 如图,以直角三角形ABC的直角边AC和斜边AB分别向外作正方形,其中正方形的面积如图所示,则三角形AED的面积是30.
如图,以直角三角形ABC的直角边AC和斜边AB分别向外作正方形,其中正方形的面积如图所示,则三角形AED的面积是30.