题目内容
4.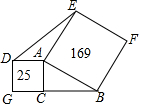 如图,以直角三角形ABC的直角边AC和斜边AB分别向外作正方形,其中正方形的面积如图所示,则三角形AED的面积是30.
如图,以直角三角形ABC的直角边AC和斜边AB分别向外作正方形,其中正方形的面积如图所示,则三角形AED的面积是30.
分析 直接利用全等三角形的判定和性质得出△ANE≌△ACB(AAS),进而结合勾股定理得出EN的长,即可得出答案.
解答 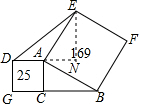 解:过点E作EN⊥DA于点N,
解:过点E作EN⊥DA于点N,
∵∠EAN+∠NAB=90°,
∠NAB+∠CAB=90°
∴∠EAN=∠CAB,
在△ANE和△ACB中,
$\left\{\begin{array}{l}{∠ENA=∠ACB}\\{∠NAE=∠CAB}\\{AE=AB}\end{array}\right.$,
∴△ANE≌△ACB(AAS),
∴AN=AC=5,
由题意可得:AD=5,AB=AE=13,
∴BC=EN=12,
∴S△DAE=$\frac{1}{2}$×EN×AD=$\frac{1}{2}$×5×12=30.
故答案为:30.
点评 此题主要考查了全等三角形的判定和性质和勾股定理,正确得出EN的长是解题关键.

练习册系列答案
相关题目
16.用反证法证明“三角形的三个外角中至多有一个锐角”,应先假设( )
| A. | 三角形的三个外角都是锐角 | |
| B. | 三角形的三个外角和至少有两个锐角 | |
| C. | 三角形的三个外角中没有锐角 | |
| D. | 三角形的三个外角中至少有一个锐角 |