Question

18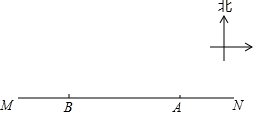．舟山市朱家尖南沙是一处游泳避暑的好地方．海岸线MN上有两个观察台A、B，A在B的正东方向，AB=400米．从A测得一个游泳者在北偏西60°方向，从B测得这个游泳者在北偏东45°方向．
（1）在图中画出这个游泳者点C的位置，并标出相关的角度．
（2）求点C到海岸线MN的距离．（结果保留根号）
（3）若这个游泳者从点C处沿射线AC的方向游一段时间后，到达D处，此时，从B测得这个游泳者在北偏西15°的方向，若景区规定游泳者到海岸线MN的距离超过250米，就要发出警告．问观察台是否要对游泳者发出警告？请说明理由．

Answer 1

分析 （1）根据方向角的定义作出图形即可得；
（2）作CE⊥AB，可得BE=CE=x，AE=$\frac{CE}{tan∠CAE}$=$\sqrt{3}$x，由BE+AE=AB列出方程求得x的值即可得；
（3）作BG⊥AD、DF⊥AB，求出BG=$\frac{1}{2}$AB=200，AG=$\frac{\sqrt{3}}{2}$AB=200$\sqrt{3}$，根据DG=BG=200可得AD=200$\sqrt{3}$+200，由DF=$\frac{1}{2}$AD即可作出判断．

解答 解：（1）如图所示：


（2）过C作CE⊥AB于E，
设CE=x，
∵∠CBA=45°，
∴BE=CE=x，
∵∠CAE=90°-60°=30°，
∴AE=$\frac{CE}{tan∠CAE}$=$\frac{x}{\frac{\sqrt{3}}{3}}$=$\sqrt{3}$x，
∵BE+AE=AB，
∴$x+\sqrt{3}x=400$，
解得：x=$CE=200（\sqrt{3}-1）=200\sqrt{3}-200$；

（3）过B作BG⊥AD于G，过D作DF⊥AB于F．
∵AB=400，∠BAC=30°，
∴BG=200，AG=200$\sqrt{3}$．
又∵∠BDC=45°，
∴DG=BG=200，
∴AD=200$\sqrt{3}$+200．
在Rt△ADF中，DF=$\frac{1}{2}AD$=100$\sqrt{3}$+100＞250．
∴观察台要对游泳者发出警告．

点评 本题考查了解直角三角形的应用-方向角问题．通过作辅助线，构造直角三角形是解题的关键．