题目内容
7. 如图,在△ABC中,∠ACB=90°,AC=2,BC=2$\sqrt{3}$,D是BC边上一点,直线ED⊥BC于点D,交AB于点E,CF∥AB交直线DE于点F,设CD=x
如图,在△ABC中,∠ACB=90°,AC=2,BC=2$\sqrt{3}$,D是BC边上一点,直线ED⊥BC于点D,交AB于点E,CF∥AB交直线DE于点F,设CD=x(1)当x取何值时,四边形EACF是菱形?请说明理由;
(2)当x取何值时,四边形EACD的面积等于$\frac{2}{3}$$\sqrt{3}$?
分析 (1)首先证明∠B=30°,四边形AEFC是平行四边形,当AC=AE=2时,四边形AECF是菱形,推出AE=EB=2,由ED∥AC,推出CD=BD=$\sqrt{3}$;
(2)由S△ABC=$\frac{1}{2}$×2×2$\sqrt{3}$=2$\sqrt{3}$,S四边形AEDC=$\frac{2\sqrt{3}}{3}$,推出S△BDE=2$\sqrt{3}$-$\frac{2}{3}$$\sqrt{3}$=$\frac{4\sqrt{3}}{3}$,推出$\frac{1}{2}$•(2$\sqrt{3}$-x)•$\frac{2\sqrt{3}-x}{\sqrt{3}}$=$\frac{4\sqrt{3}}{3}$,解方程即可;
解答 解:(1)在Rt△ABC中,∵∠ACB=90°,AC=2,BC=2$\sqrt{3}$,
∴tan∠B=$\frac{2}{2\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠B=30°,
∴AB=2AC=4,
∵∠ACB=∠BDE=90°,
∴AC∥EF,∵CF∥AE,
∴四边形AEFC是平行四边形,
∴AC=AE=2时,四边形AECF是菱形,
∴AE=EB=2,
∵ED∥AC,
∴CD=BD=$\sqrt{3}$,
∴x=$\sqrt{3}$时,四边形AEFC是菱形.
(2)∵S△ABC=$\frac{1}{2}$×2×2$\sqrt{3}$=2$\sqrt{3}$,S四边形AEDC=$\frac{2\sqrt{3}}{3}$,
∴S△BDE=2$\sqrt{3}$-$\frac{2}{3}$$\sqrt{3}$=$\frac{4\sqrt{3}}{3}$,
∴$\frac{1}{2}$•(2$\sqrt{3}$-x)•$\frac{2\sqrt{3}-x}{\sqrt{3}}$=$\frac{4\sqrt{3}}{3}$,
解得x=2$\sqrt{3}$-2$\sqrt{2}$ 或2$\sqrt{3}$+2$\sqrt{2}$(舍弃),
∴x=2$\sqrt{3}$-2$\sqrt{2}$.
点评 本题考查平行四边形的判定和性质、菱形的判定和性质、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A型 | B型 | |
| 价格(万元/台) | 12 | 10 |
| 处理污水量(吨/月) | 240 | 200 |
(2)在(1)的条件下,若每月要求处理的污水量不低于2040吨,为了节约资金,请你为该厂设计一种最省钱的购买方案.
| A. | y1<y2<y3 | B. | y1>y2>y3 | C. | y2<y3<y1 | D. | y3>y2>y1 |
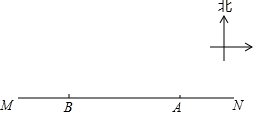 舟山市朱家尖南沙是一处游泳避暑的好地方.海岸线MN上有两个观察台A、B,A在B的正东方向,AB=400米.从A测得一个游泳者在北偏西60°方向,从B测得这个游泳者在北偏东45°方向.
舟山市朱家尖南沙是一处游泳避暑的好地方.海岸线MN上有两个观察台A、B,A在B的正东方向,AB=400米.从A测得一个游泳者在北偏西60°方向,从B测得这个游泳者在北偏东45°方向.
 已知抛物线y=ax2-2x+c的对称轴为直线x=-1,顶点为A,与y轴正半轴交点为B,且△ABO的面积为1.
已知抛物线y=ax2-2x+c的对称轴为直线x=-1,顶点为A,与y轴正半轴交点为B,且△ABO的面积为1.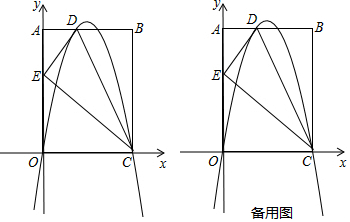
 如图,在平面直角坐标系中,顶点为(-4,1)的抛物线交y轴于A点,交x轴于B、C两点(点B在C的右侧),已知A点坐标为(0,-3).
如图,在平面直角坐标系中,顶点为(-4,1)的抛物线交y轴于A点,交x轴于B、C两点(点B在C的右侧),已知A点坐标为(0,-3).