题目内容
8. 如图,已知菱形ABCD,E是对角线BD上一点,用尺规在BD上确定一点F,使得∠CFD=∠AEB,并说明理由.(保留作图痕迹,不写作法)
如图,已知菱形ABCD,E是对角线BD上一点,用尺规在BD上确定一点F,使得∠CFD=∠AEB,并说明理由.(保留作图痕迹,不写作法)
分析 在DB上截取DF=BE,连接CF,则∠CFD=∠AEB;
由菱形的性质得到AB∥CD,AB=CD,根据平行线的性质得到∠CDF=∠ABE,可证得△ABE≌△CDF,由全等三角形的性质有∠CFD=∠AEB.
解答  解:作图如图所示;
解:作图如图所示;
证明:由作图得BE=DF,
∵四边形ABCD是菱形,
∴AB∥CD,AB=CD,
∴∠CDF=∠ABE,
在△ABE和△CDF中,$\left\{\begin{array}{l}{BE=DF}\\{∠ABE=∠CDF}\\{AB=CD}\end{array}\right.$,
∴△ABE≌△CDF,
∴∠CFD=∠AEB.
点评 本题主要考查了尺规作图,菱形的性质,平行线的性质,全等三角形的判定与性质,掌握尺规作图的基本方法是解题的关键.

练习册系列答案
相关题目
19.若(m-n)(m-n-2)-8=0,则m-n的值为( )
| A. | 4或-2 | B. | 4 | C. | -2 | D. | 2 |
13. 如图,直线l1、l2与直线l3相交,若l1∥l2,∠1=120°,则∠2=( )
如图,直线l1、l2与直线l3相交,若l1∥l2,∠1=120°,则∠2=( )
 如图,直线l1、l2与直线l3相交,若l1∥l2,∠1=120°,则∠2=( )
如图,直线l1、l2与直线l3相交,若l1∥l2,∠1=120°,则∠2=( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
17.某厂决定购买10台污水处理设备.现有A、B两种型号的设备,其中每台的价格,月处理污水量如表:
(1)经预算:治污部门购买污水处理设备的资金不超过105万元,你认为该部门有哪几种购买方案?
(2)在(1)的条件下,若每月要求处理的污水量不低于2040吨,为了节约资金,请你为该厂设计一种最省钱的购买方案.
| A型 | B型 | |
| 价格(万元/台) | 12 | 10 |
| 处理污水量(吨/月) | 240 | 200 |
(2)在(1)的条件下,若每月要求处理的污水量不低于2040吨,为了节约资金,请你为该厂设计一种最省钱的购买方案.
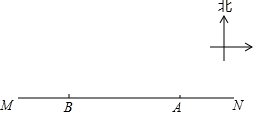 舟山市朱家尖南沙是一处游泳避暑的好地方.海岸线MN上有两个观察台A、B,A在B的正东方向,AB=400米.从A测得一个游泳者在北偏西60°方向,从B测得这个游泳者在北偏东45°方向.
舟山市朱家尖南沙是一处游泳避暑的好地方.海岸线MN上有两个观察台A、B,A在B的正东方向,AB=400米.从A测得一个游泳者在北偏西60°方向,从B测得这个游泳者在北偏东45°方向.