题目内容
10.(1)计算($\sqrt{5}$-π)0-6tan30°+($\frac{1}{2}$)-2+|1-$\sqrt{3}$|(2)先化简,再求值.
$\frac{12}{{m}^{2}-9}$+$\frac{2}{3-m}$(其中m是绝对值最小的实数)
分析 (1)原式利用零指数幂法则,特殊角的三角函数值,负整数指数幂法则,以及绝对值的代数意义化简,计算即可得到结果;
(2)原式通分并利用同分母分式的减法法则计算,得到最简结果,求出m的值代入计算即可求出值.
解答 解:(1)原式=1-2$\sqrt{3}$+4+$\sqrt{3}$-1=4-$\sqrt{3}$;
(2)原式=$\frac{12}{(m+3)(m-3)}$-$\frac{2(m+3)}{(m+3)(m-3)}$=$\frac{-2(m-3)}{(m+3)(m-3)}$=-$\frac{2}{m+3}$,
由题意得到m=0,
则原式=-$\frac{2}{3}$.
点评 此题考查了分式的化简求值,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
2.如果点P1(x1,y1),P2(x2,y2),P3(x3,y3)在某双曲线上,且x1<x2<0<x3,则y1,y2,y3的大小关系可能为( )
| A. | y1<y2<y3 | B. | y1>y2>y3 | C. | y2<y3<y1 | D. | y3>y2>y1 |
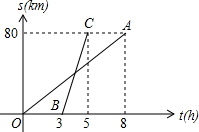 如图,已知自行车与摩托车从甲地开往乙地,OA与BC分别表示它们与甲地距离s(千米)与时间t(小时)的关系,则:
如图,已知自行车与摩托车从甲地开往乙地,OA与BC分别表示它们与甲地距离s(千米)与时间t(小时)的关系,则: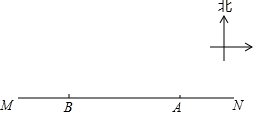 舟山市朱家尖南沙是一处游泳避暑的好地方.海岸线MN上有两个观察台A、B,A在B的正东方向,AB=400米.从A测得一个游泳者在北偏西60°方向,从B测得这个游泳者在北偏东45°方向.
舟山市朱家尖南沙是一处游泳避暑的好地方.海岸线MN上有两个观察台A、B,A在B的正东方向,AB=400米.从A测得一个游泳者在北偏西60°方向,从B测得这个游泳者在北偏东45°方向. 如图,AB∥CD,∠E+∠G=∠H,则∠A+∠B+∠C+∠D+∠F的度数为360°.
如图,AB∥CD,∠E+∠G=∠H,则∠A+∠B+∠C+∠D+∠F的度数为360°.